No one believed him. Not even fellow mathematicians. They thought he was wrong. They thought he was crazy. Even he ended up doubting himself and went crazy. And yet, he had mathematically proved it all. Georg Cantor had figured out how to manipulate the infinite. Even more remarkable, he showed that there were actually several infinities; and some are bigger than others!

In an effort to make mathematics more computable, a consortium of today's greatest mathematicians have laid out new foundations. Amazingly, they all lie upon one single axiom, called univalence. The goal of this axiom is to make formal mathematics more similar to informal mathematics. With univalence, our Arabic numbers aren't just like natural numbers; They are natural numbers. Univalence also has unforeseen and mesmerizing consequences.

In this article, we explore the possibilities allowed by higher inductive types. They enable a much more intuitive formalization of integers and new mind-blowing definitions of the (homotopical) circle and sphere.

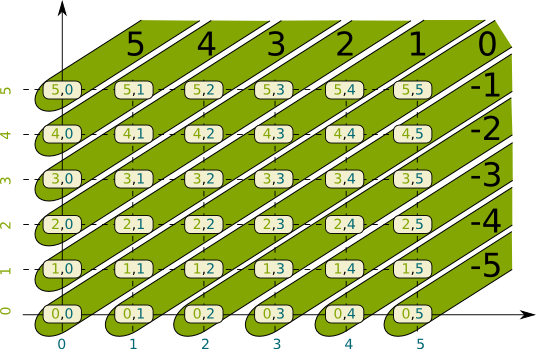
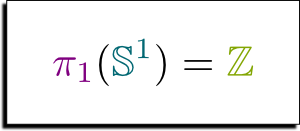In 2013, three dozens of today's brightest minds have just laid out new foundation of mathematics after a year of collective effort. This new paradigm better fits both informal and computationally-checkable mathematics. There is little doubt that it will fundamentally change our perspective on rigorous knowledge, and it could be that, in a few decades, the book they published turns out to be the bedrock of all mathematics, and, by extension, all human knowledge! Have a primer of this upcoming revolution, with this article on type theory, the theory that the book builds upon!

Although they have been used for thousands of years, an actual definition of numbers was given less than a century ago! From the most fundamental level of set theory, this article takes you to the journey of the construction of natural, integer, rational, real and complex numbers.

Although highly appreciated by artists, self-reference has been a nightmare for mathematicians. It took one of the greatest, Kurt Gödel, to provide a better understanding of it. This article deals with paradoxes, recursion, fractals and Gödel's incompleteness theorems.