Tag Archives: Computer Science
Mathematical Physics, Determinism, Game of Life (Hiking in Modern Math 6/7)
Chaos Theory, Meteorology, Navier-Stokes, Wolfram (Hiking in Modern Math 5/7)
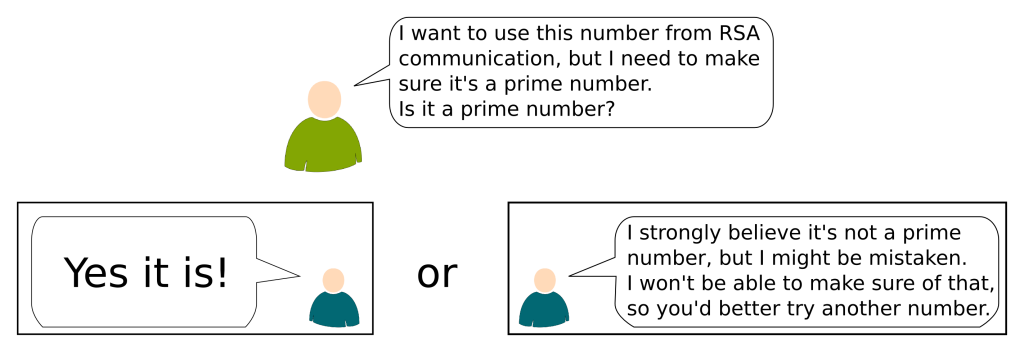
Complexity Theory, P versus NP, RSA Cryptography (Hiking in Modern Math 2/7)
Theory of Computation, Turing Machine (Hiking in Modern Math 1/7)
Shannon’s Information Theory (Trek through Math 5/8)
Univalent Foundations of Mathematics
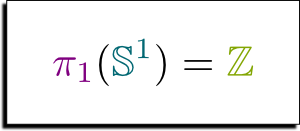
Homotopy Type Theory and Higher Inductive Types

Type Theory: A Modern Computable Paradigm for Math

The Tortuous Geometry of the Flat Torus

The New Big Fish Called Mean-Field Game Theory

Numbers and Constructibility

Shannon’s Information Theory

Cryptography and Quantum Physics

Bayesian Games: Math Models for Poker

Probabilistic Algorithms, Probably Better
Web Programming: From HTML to AJAX

P versus NP: A Crucial Open Problem
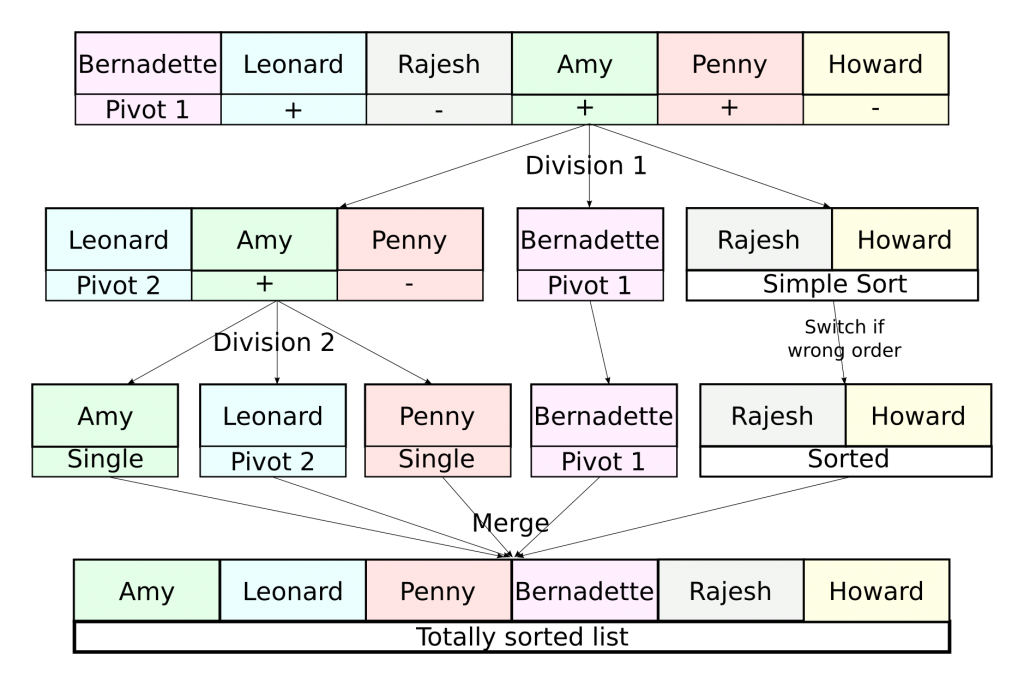
From Divide and Conquer to Parallelization