The New Big Fish Called Mean-Field Game Theory

Many people believe that mathematics research is over. Yet, as I often retort to them, we still only know little of the immense ocean of mathematical structures, which, yet, fill the world we live in. One recent advancement is that of mean-field games around 2006, independently by Minyi Huang, Roland Malhamé and Peter Caines in Montreal, and by Jean-Michel Lasry and Fields medalist Pierre-Louis Lions in Paris. This revolutionary model has since been greatly developed by other mathematicians and largely applied to describe complex multi-agent dynamic systems, like Mexican waves, stock markets or fish schoolings.

Applications of mean-field games go way beyond the realm of animal swarms! Recently, Lasry and Lions exploited mean-field game theory to design new decision making processes for financial, technological and industrial innovation, as they launched the company mfg labs in Paris! Customers include banks and energy councils.

I need to thank Viswanadha Puduru Reddy and Dario Bauso for having taught me the basics of mean-field games I’ve presented here! I’m also glad to announce that Roland Malhamé, one of the founders of mean-field games, has read and appreciated this article.

The Main Idea

Sometimes large numbers are much simpler than small ones. The core idea of mean field games is precisely to exploit the smoothing effect of large numbers. Indeed, while game theory struggles with systems of more than 2 individuals, mean-field games turn the problem around by restating game theory as an interaction of each individual with the mass of others.

What do you mean?

Imagine a fish in a schooling. In classical game theory, it reacts to what other fishes nearby do. And this is very complicated, as there is then a huge number of interactions between the different fishes. This means that classical game theory corresponds to a long list of highly coupled equations. Don’t worry if you don’t get what I mean. In essence, my point is that the classical game theory model becomes nearly impossible to solve with as little as 3 fishes, and it gets “exponentially harder” with more fishes.

I’m using very loosely the concept of “exponentially harder” here! That’s not good and you should not do that! But, basically, a way of understanding that is that the number of states grows exponentially in the number of fishes.

So, how are things in mean-field game theory?

They are cleverly thought! In mean-field game theory, each fish does not care about each of the other fishes. Rather, it cares about how the fishes nearby, as a mass, globally move. In other words, each fish reacts only to the mass. And, amazingly, this mass can be nicely described using the powerful usual tools of statistical mechanics!

But how do we know what the mass does?

Granted, the motion of the mass is necessarily the result of what each fish does. This means that we actually still have coupled equations, between each fish and the mass.

On one hand, the reaction of fishes to the mass is described to the Hamilton-Jacobi-Bellman equation. On the other hand, the aggregation of the actions of the fishes which determines the motion of the mass corresponds to the Fokker-Planck-Kolmogorov equation. Mean-field game theory is the combination of these two equations.

Waw! This sounds scary…

Don’t worry, it sounds way more complicated than it really is! Bear with me!

Hamilton-Jacobi-Bellman

Before getting further, I need to have you pondering upon a simple question… What can fishes do?

They can move however they want, can’t they?

I’m not sure Newton would have liked this answer… Isn’t it rather acceleration that’s in their control?

Oh yeah. And there’s also the water currents…

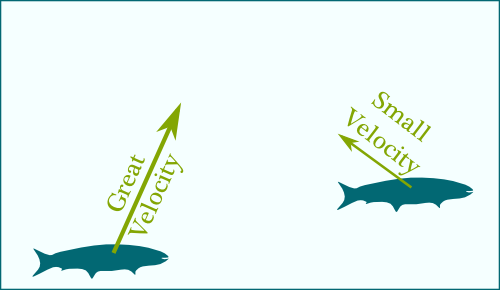
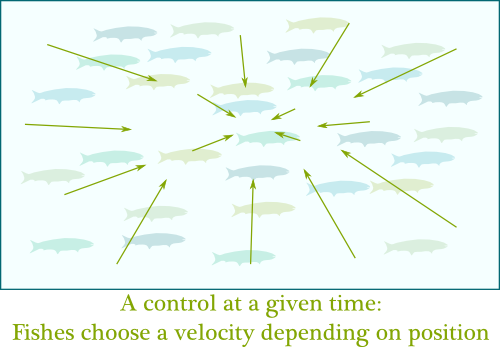
Humm… This is getting complicated. So, let’s assume that, as you first said, fishes can move however they want. Mathematically, this means that they control their velocity, which is an arrow which points towards their direction of motion. Plus, the longer the arrow the faster fishes swim. So, at any time, a fish controls its velocity, depending on where it is, and where the mass is.

Where are you going with this?

I’m going to define one of the two main objects of mean-field games: the control $u$. A control is a choice of velocity depending on position and time. Crucially, if all fishes are similar, then they all have the same optimal control. Thus, we only need one control $u$ to describe the actions of all the fishes!

Formally, fishes live in a space $\mathbb R^n$ (or even, a manifold), with $n=3$ for the case of real fishes. Denoting $x \in \mathbb R^n$ the position and $t \in \mathbb R$ the time, then a control is a map $u : \mathbb R^n \times \mathbb R \rightarrow \mathbb R^n$, where $u(x, t) \in \mathbb R^n$ is the velocity chosen by a fish located at position $x$ at time $t$.

What do you mean by “optimal control”?

Hummm… The concept of what’s a best control for fishes is quite debatable. But, for simplicity, let’s say that a good control should get fishes close to the schooling where it is safer, while avoiding abusing great velocities which are fuel-consuming.

In fact, the similarity of fishes I mentioned earlier means that if two fishes are at the same location at the same time, then they’ll feel the same unsafeness, and that if they choose the same velocities, then they’ll pay the same cost of abusing of that velocity.

Crucially, a good control doesn’t only care about what’s best for the fish right now. It must also consider where the fish should go for it to be safe in the future.

How is that modeled?

Basically, at each point of time, a fish pays the unsafeness of its position and the exhaustion due to its velocity. Its total loss over all time simply consists in adding up all the losses at all times. Thus, the fish must strike a happy balance between hurrying to reach a future safer position and not running out of energy at present time. This setting is known as an optimal control problem.

The unsafeness of fish is typically modeled by a cost $g(x,m)$ which depends on the position $x$ of the fish and on the “position” $m$ of the mass (which I’ll explain more about later). Meanwhile, there is a “fuel-consuming” cost due to velocity. Quite often, this velocity cost is modeled by kinetic energy, which equals $^1/_2 ||u||^2$ (more or less a multiplicative factor). The cost over all times is then $\int_t (^1/_2 ||u||^2 + g(x,m)) dt$. In finite horizon, there may also be a cost $G(x, m)$ for the positions of the fish and the mass at end time $T$. Also, I should say that control problems can get awfully more complicated than the setting I’m defining here, and that a whole article should be written about them. If you can, please write it!

So, how do you solve the optimal control problem?

Optimal control is solved like chess! In essence, we should first think of where we should get to, and then work backwards to determine which steps will get us there. This is what’s known as dynamic programming.

Shouldn’t it rather be called something like “backward programming”?

I totally agree with you. But I don’t name stuffs!

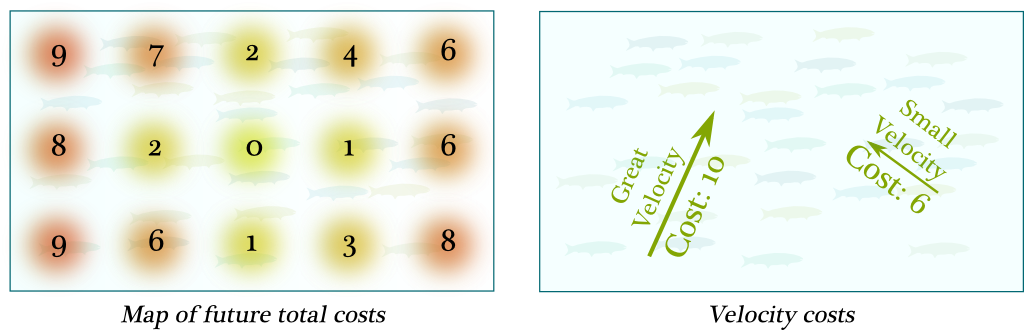
So how does dynamic programming solve the optimal control problem?

First, we start by judging how costly the possible future positions are. This gives us a map of total future costs. Now, ideally, no matter where a fish is, he’d prefer to get to the least costly future position. However, there’s also a cost due to motion:

Now, given a present position, we’ll want to choose a velocity which minimizes the sum of future total costs and velocity cost.

Humm… Can you give an example?

Sure! Look at the figure below. On the left, the present position is assumed to be where arrows go out from. Staying still has a future total cost of 4, and no velocity cost. Meanwhile, moving one step to the left yields a future total cost of 2 and a velocity cost of 2, which add up to 4. What’s more, moving one step below adds a future total cost of 1 and a velocity cost of 2, adding up to 3. Thus, moving below is less costly than moving to the left or staying still. In fact, it’s the least costly move. This is why the optimal control consists in moving downwards. Interestingly, now that we know what the optimal control at the present position is, we can derive the present total cost, which is the sum of present unsafeness (1), future total cost (1) and velocity cost (2): 4.

Now, by doing so for all present positions, we can derive the full optimal control at present time, as well as the map of present total costs!

Notice that the left picture is the future, from which we deduce the present on the right. This is why I’d rather rename dynamic programming as backward programming. In fact, in mean-field games, the Hamilton-Jacobi-Bellman equation is often informally called the backward equation.

Wait a minute… Does dynamic programming mean that we need to discretize space and time?

Excellent remark! Well, by increasing the details of discretization, and following Newton’s steps, we can in fact derive a continuous version of dynamic programming. This yields the famous Hamilton-Jacobi-Bellman equation, which, in essence, is simply the continuous extension of dynamic programming!

Denoting $J(x,t)$ the unsafeness of being at position $x$ at time $t$, the choice of velocity at position $x$ and time $t$ must minimize $(\partial_t J + u \cdot \nabla_x J) + (^1/_2||u||^2) + g(x,m)$. The first term corresponds to total future cost (in future position), the second to the velocity cost, and the last one to present unsafeness. If you’re unfamiliar with derivatives, check my article on differential calculus.

Fokker-Planck-Kolmogorov

So, if I recapitulate, the Hamilton-Jacobi-Bellman tells us how fishes react to the mass. But, as we’ve already discussed it, the mass is derived from what the fishes do.

Wait… What do you mean by “the mass $m$”?

Excellent question! The mass $m$ describes all trajectories of all fishes.

Waw! That sounds like a scary object!

There’s a way to make it sound (slightly) less frightening: Let’s imagine all the possible trajectories. Then, we can simply have $m(x,t)$ counting the ratio of fishes which happen to be at position $x$ at time $t$.

To be more accurate, $m(\cdot,t)$ is rather a probability distribution over the space $\mathbb R^n$ fishes live in. But, to obtain differential equations, mean-field games usually assume that this distribution can be described by a probability density function $\mathbb R^n \rightarrow \mathbb R, x \mapsto m(x, t)$.

Now, as opposed to the backward Hamilton-Jacobi-Bellman equation, we are now going to work forward: We’ll derive the mass of the near future, from the present mass and the control.

How do we do that?

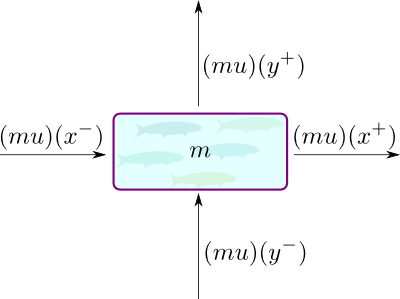
We first need to notice that the velocities given by the control aren’t very relevant to describe how the mass moves. Instead, as noticed by statistical mechanics, what rather matters is the “quantity of motion” of fishes, which physicists call momentum. This momentum really is what describes how fishes move. At a given point, this momentum corresponds to the velocity multiplied by the number of fishes in motion. It is thus the vector field $m(x,t) \cdot u(x,t) = (mu) (x,t)$. Now, by adding up all the quantities going in and out of a point we obtain the Liouville equation.

Sparing you the details, what we get is that everything that goes out and in of our point adds up to $div(mu) = \sum \partial_{x_i}(mu)$. This means that the variation of the mass is $\partial_t m = – div(mu)$, which is the Liouville equation.

But the Liouville equation features no Brownian motion.

Brownian motion?

Yes, I need to explain that! The thing is that, if fishes follow the Liouville equation, they’ll all end up converging to the single safest point. That’s not what happens in reality. While fishes would probably like to all be in the middle of the schooling, there may not get a chance, as the crowdedness will have them knocking one another. One way of interpreting that, is to say that they won’t be in total control of their trajectories, kind of like a grain of pollen floating in water.

In fact, this motion of the grains of pollen was discovered by botanist Robert Brown in 1827, and it is what we now call the Brownian motion. This Brownian motion has played a key role in the History of science, as it was what led Albert Einstein to prove the existence of atoms! This is what I explained it in my talk More Hiking in Modern Math World:

For our purpose, the important effect of Brownian motion is that there is a natural tendency for fishes to go from crowded regions to less crowded ones. Thus, while safeness makes fishes converge to a single safest point, the Brownian motion spreads them in space. The addition of the latter idea to the Liouville equation yields by the famous Fokker-Planck equation, also known as the Kolmogorov forward equation, and which I’ll name the Fokker-Planck-Kolmogorov equation here.

The relative crowdedness of a point compared to its surrounding is measured by the Laplacian $\Delta_x m = \sum \partial_{x_i x_i}^2 m$. Thus, the Fokker-Planck-Kolmogorov equation is then $\partial_t m = – div(mu) + ^{\sigma^2}/_2 \Delta_m$, where $\sigma$ represents the strength of the Brownian motion. More precisely, it is the standard deviation of the Brownian motion in one unit of time (typically, in meters/second).

Time-Independency

One natural setting in which to study mean-field games is that where there is a perfect symmetry in time. This means that the costs $g$ don’t depend in time and that there is no end time.

No end time?

I know, it sounds weird. After all, fishes eventually die, so there has to be an end time. But if this end time is so far away compared to the reaction time scales of the fishes, and it’s the case in practice, then it’s very natural to approximate the very large end time by infinity.

There are two main modelings of this time-independent infinite horizon setting. First is to consider that the total cost is the average cost, which means that $J = \lim_{T \rightarrow \infty} \; ^1/_T \int_0^T (^1/_2 ||u||^2 + g(x,m)) dt$. Second is to involve a discount rate, which says that the present counts more than the future. Denoting $\rho > 0$ this discount rate, we’d have $J = \int_0^\infty e^{-\rho t} (^1/_2 ||u||^2 + g(x,m)) dt$. Interesting, differentiating this latter formula can be done analytically.

So how does that affect mean-field games?

Crucially, now, the controls $u$ no longer depend on the time variable. They are just instructions that give a velocity to be taken depending on position. This means that, at each point of space, there is a velocity to take. This is what physicists call a vector field.

Does the same hold for the mass?

Absolutely! The mass is now merely described by an unchanging variable $m$. This means that the mass of fishes is remaining still. Or, rather, since this is up to switch of inertial system, that fishes are moving altogether at the same velocity (up to Brownian motion, and along the current to minimize kinetic energy).

But what about changes of direction of the fish schooling?

Hehe… That’s an awesome question. Well, we’d need to get back to the time-dependent case, and include some perturbations of the map of unsafeness, which may be due, for instance, to the apparition of a predator! I’ve never seen simulations of that, but I trust the maths to make it awesome!

Linear-Quadratic Games

In this article, whenever I gave formulas so far, I assumed we were in a (nearly) linear-quadratic setting. This means that the control linearly determine the velocity (like in the formula $u=\dot x$, or more generally, if $u=a\dot x + b$`), that the cost of velocity is quadratic (as in the kinetic energy $^1/_2 ||u||^2$), and that the unsafeness of position is also quadratic (which, in fact, we don’t need to state the theorems of this last section). Crucially, this makes the Hamilton-Jacobi-Bellman equation easy to transform into a partial differential equation.

Namely, removing constant terms, it yields $\min\; ^1/_2 ||u||^2 + u \cdot \nabla_x J$, hence $u = -\nabla_x J$. Thus, we obtain, after including also the Brownian motion, the partial differential equation on $J$ defined by $-\partial_t J + \;^1/_2 ||\nabla_x J||^2 – \;^{\sigma^2}/_2 \Delta J = g(x,m)$. In the time-independent setting with discount rate $\rho$, we get $^1/_2 ||\nabla_x J||^2 – \;^{\sigma^2}/_2 \Delta J + \rho J = g(x,m)$.

Not only do these assumptions enable us to write nice-looking partial differential equations, they also imply three holy results mathematicians are always searching for.

To be precise, the three results I’ll present require assumptions on the boundedness and regularity of cost functions $g$ at all time and $G$ at end time, and on the mass $m$ at time 0. Namely, $g$ and $G$ must be uniformly bounded and Lipschitz-continuous, while $m$ at time 0 must be absolutely continuous with regards to Lebesgue measure (i.e. it must correspond to a classical probability density function).

What are the three holy results?

The two first ones are very classical. Yes, you know what I’m talking about: existence and uniqueness.

Why are these so important?

Because, if we want our equations to have a chance to describe reality, then their solutions must share one important feature with reality. Namely, they must exist, and they must be unique. More generally, especially in the field of partial differential equations, existence and uniqueness of solutions often represent the Saint-Graal, or, at least, an important mathematical question.

Really? Don’t people care about solving these?

Sure, people do! But since these equations usually can’t be solved analytically, we usually turn towards numerical simulations. These simulations typically discretize space and time and approximate the equations. However, while these numerical simulations will run and engineers may then make decisions based on their outcomes, if the equations didn’t have a solution to start with, or if they had several of them, then the results of the simulations would then be meaningless! Proving existence and uniqueness yields evidence for the relevancy of numerical simulations.

I should point out that numerical simulations may still go wrong even though a partial differential equation does satisfy existence and uniqueness. Numerical simulations can be quite a tricky endeavor. If you can, please write about finite difference, finite element and finite volume methods!

In fact, one of the 7 Millenium Prize problem, called the Navier-Stokes existence and smoothness problem, is precisely about determining the existence and uniqueness of solutions to a partial differential equation, as I explain it later in my talk More Hiking in Modern Math World:

Each Millenium Prize problem is worth 1 million dollars. And, apparently, Kazakh mathematician Mukhtarbay Otelbayev has claimed the Prize for the Navier-Stokes existence and smoothness problem! However, it may take a while for his proof to be translated, reviewed and accepted… provided it is correct!

But what about the mean-field game partial differential equations? Do they satisfy existence and uniqueness?

In the linear-quadratic setting with Brownian motion, they do! How cool is that?

I guess it’s nice… So, what about the third result?

The third result is that the solutions can be computed! While classical partial differential equations are solvable by numerical methods, mean-field game equations are a bit trickier as they form coupled partial differential equations. More precisely, given the mass $m$, we can compute the optimal control $u$ with the Hamilton-Jacobi-Bellman equation; and given the control $u$, we can derive the mass $m$ from the Fokker-Planck-Kolmogorov equation. But, at the beginning, we don’t know any of the two variables!

So how can we compute any of them?

Through an iterative process! Let’s start with an arbitrary mass $m_0$.

Careful! The mass $m_0$ must not be confused with the mass $m(\cdot, 0)$ at time 0. Rather, $m_0 : \mathbb R^n \times \mathbb R \rightarrow \mathbb R_+$ is an arbitrary mass defined for all positions and all times. It is the first mass of our iteration process.

Then, we’ll compute the corresponding optimal control $u_1$, from which we then derive the mass $m_1$. And we repeat this process to determine $u_2$ and $m_2$, then $u_3$ and $m_3$… and so on. Crucially, this iterative process will yield the right result, as, in some sense I won’t develop here, the sequence $(u_n, m_n)$ converges exponentially quickly to the unique solution $(u,m)$ of the mean-field game couple partial differential equations!

In essence, this is a consequence of the contraction property of the map $(u_n, m_n) \mapsto (u_{n+1}, m_{n+1})$. This contraction property, by the way, is what proves the existence and uniqueness of a solution of the mean-field game coupled partial differential equation.

Let’s Conclude

It’s interesting to note that the Hamilton-Jacobi-Bellman equation comes from control theory (which is often studied in electrical and engineering departments), while the Fokker-Planck-Kolmogorov equation first appeared in statistical mechanics. And yet, it is in game theory that their combination has yielded the most relevant models! The story of the creation of mean-field game theory really is that of the power of interdisciplinarity in innovation processes! And yet, I’m confident in the fact that the full potential of mean-field games has not yet been found, and that some hidden mind-blowing applications are still to come!

I guess you want to point out, once again, that mathematics is still a mysterious ocean we’ve only started to explore…

Exactly! As weird as it sounds to many, mathematics is more than ever a living and dynamic field of research, with frequent discoveries and conceptual breakthroughs! Which leads me to advertise my own ongoing research… The first part of my PhD research is actually a generalization of mean-field games. Crucially, the key step of mean-field games occurred early in this article, as we restated classical game theory in terms of other interacting variables: The control $u$ and the mass $m$. More generally, in game theory, we can similarly decompose games into two interacting components: The strategies played by players, and the so-called return functions, which I got to name since it’s my very own creation!

What are these return functions?

Hehe! Stay tuned (by subscribing)… as I’ll reveal everything about these return functions once my (recently submitted) research paper gets published!

Comments

Prabodini says:

June 7, 2016 at 11:03 pm

Thanks, the article is really helpful and the main idea of mean field games is very well-explained.

Muhammad Saad says:

June 16, 2016 at 10:03 am

Hello Sir,

Excellent explanation, i was looking for some material on Mean field games, and i found this, once again, very neat and clean way of explanation. Its hard now a days to find some literature like this, you put way hard effort in this. Once again, the best article on mean field games.
Do share the links of your other articles in the field of game theory, or if you have a personal blog or website then please share a link. I want to explore more.
Thanks a lot !

Regards,
A Student