As computers surely take off the world, algorithms more and more rule it. I’m not saying we shall use algorithms for everything, at least not as Dr. Sheldon Cooper uses an algorithm to make friends.
Great concepts such as divide and conquer or parallelization have developed a lot and showed plenty of applications, including in the way we should deal with real life issues. Let’s mention Facebook, Youtube or Wikipedia whose success is based on these concepts, by distributing the responsibility of feeding them with contents. But, what’s less known is that astronomy also went distributed, as it has asked for every one to contribute to its development by classifying galaxy on this website. Let’s also add Science4All to that list (we’ll get there!), which counts on each and everyone of you, not only to contribute by writing articles, but also to share the pages and tell your friends!
But what has come is nothing compare to what’s coming. In his book Physics of the Future, the renowned theoretical physicist Michio Kaku predicts the future of computers. Today, computers have only one chip, which may be divided in two or four cores. Chips give computers their computability powers. But, in the future, chips will be so small and so cheap, that they will be everywhere, just like electricity today. Thousands of chips will take care of each and everyone of us. I’ll let you imagine the infinite possibilities of parallelization.
In this article, we’ll present how the divide and conquer approach improves sorting algorithms. Then we’ll talk about parallelization and the major fundamental problem $P=NC$.
Sorting algorithms
The problem of sorting data is crucial, not only in computer science. Imagine Sheldon wanted to hire a friend to take him to the comic store. He’d make a list of his friends, ranked by how good friends they are, then he’ll ask each friend to come with him. If the friend refuses, he’d have to go to the next friend of the list. Thus, he needs to sort his friends. This can take a while, even for Dr. Sheldon Cooper.
Even if he only has 6 friends, if he does the sorting badly, it can take him a while. For instance, he could use the bogosort: Write his friends’ names on cards, throw the cards in the air, pick them, test if they are sorted, and, if they are not, repeat from step 1. Even though this will eventually work, this will probably take a while. In means, it will take as many throws in the air as the number of ways to sort 6 friends, that is $6! = 6 \times 5 \times 4 \times 3 \times 2 \times 1 = 720$.
But don’t underestimate Dr. Cooper’s circle. In the pilot of the show, he claims to have 212 friends on MySpace (and it doesn’t even include Penny and Amy)! Sorting 212 friends will take a while. With the bogosort, it will take in means about 10281 throws in the air, which cannot be done in billions of years even with very powerful computers… Obviously, he’ll need to do it smartly.
Yes he can. At the first iteration, he’d have to look through the 212 friends. Then, if the favorite friend refuses, through the other 211 friends. Then, if the second favorite friend refuses, through the other 210 friends… and so on. In the worst case where all his friends refuse (which is a scenario Sheldon really should consider…), he’ll have to do $212+211+210+…+1$ basic operations. That is equal to $212*211/2 = 22,472$. Even for Dr. Cooper, this will take a while.
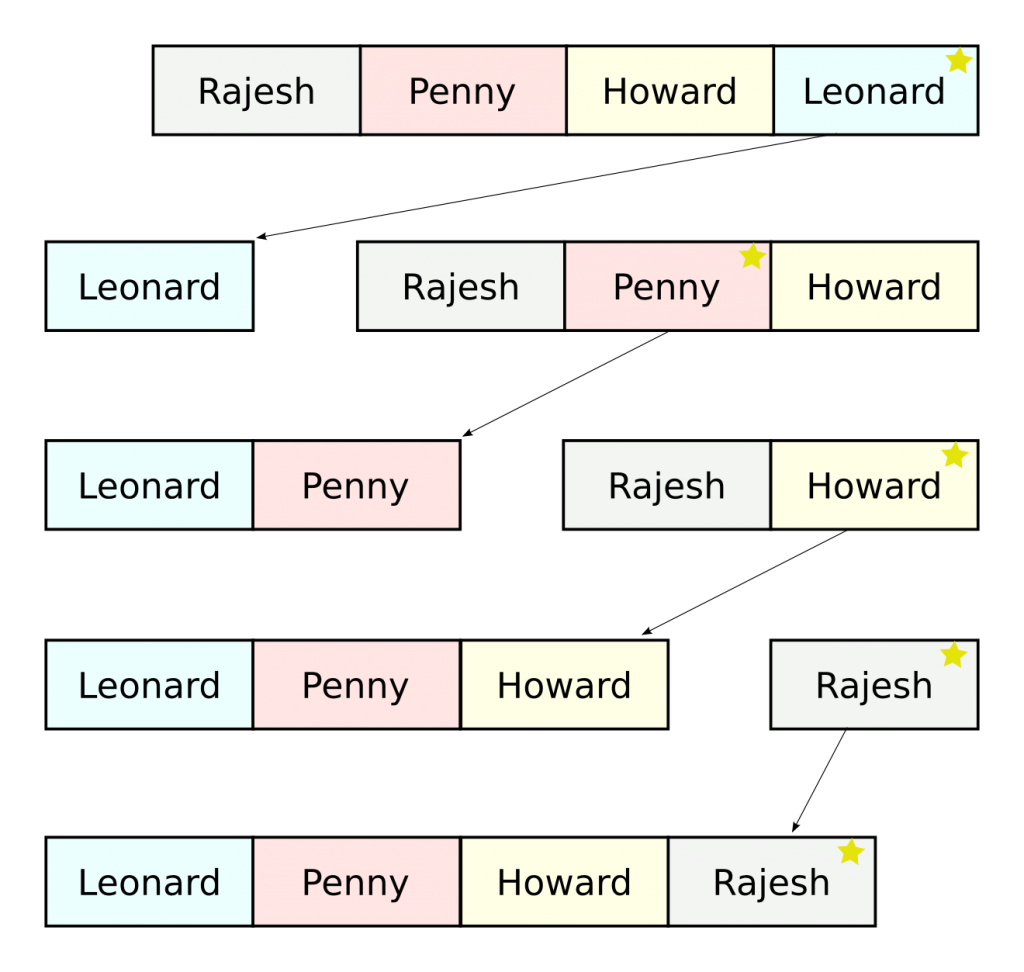
What he’s done is almost the selection sort algorithm. This algorithm uses two lists, one called the remaining list initially filled with all friends, and the other, called the sorted list, initially empty. At each iteration, the most favorite friend of the remaining list is selected and removed from that list, and it is appended to the sorted list. If the number of friends is $n$, the number of operation required for this algorithm is about $n2/2$. We say that it has a quadratic time complexity.
There are several other sort algorithms with quadratic time complexity that you can think of, including the insertion sort, the bubble sort and the gnome sort. But there are better algorithms, mainly based on the divide and conquer principle.
Divide and conquer is an extremely powerful way of thinking problems. The idea is to divide a main problem into smaller subproblems easier to solve. Solving the main problem becomes equivalent to the problems of the division into subproblems, the resolution of subproblems and the merge of results of subproblems. This is particularly powerful in the case of parallel algorithms, which I’ll get back to later in this article.
In our case, we’re going to divide the problem of sorting all of the friends into two subproblems of sorting each half of the friends. Now, there are mainly two ways of handling the dividing and merging phases. Either we focus on the dividing phase and we’ll be describing the quick sort, or we focus on the merging phase and this will lead us to the merge sort. Although I actually prefer the merge sort (and I’ll explain why later), I will be describing the quick sort.
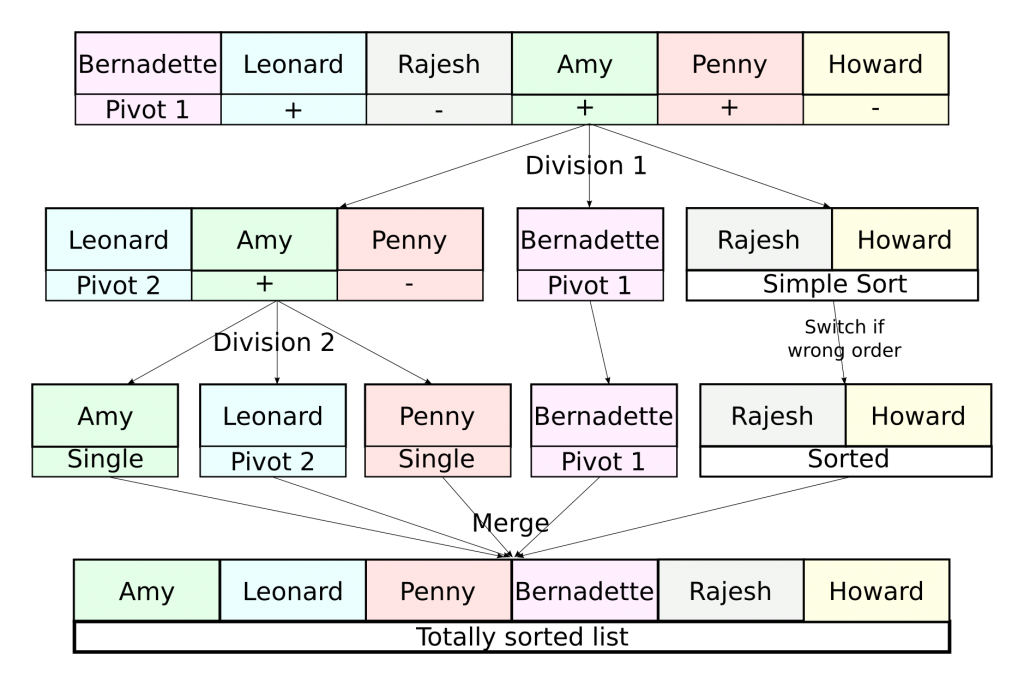
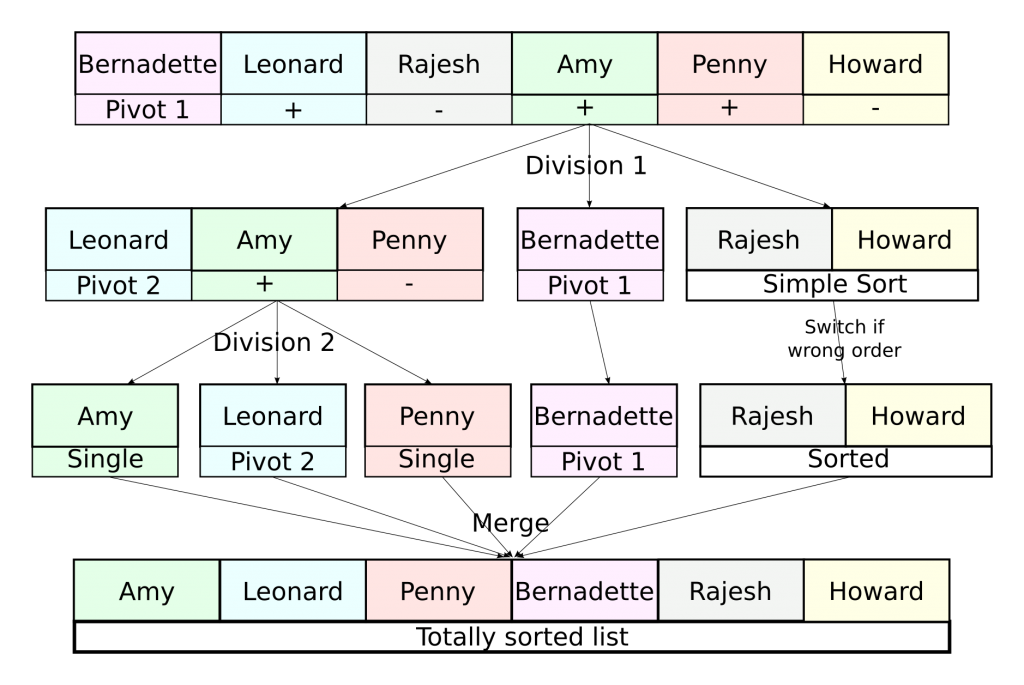
As I said, the idea of the quick sort is to focus on the dividing phase. What we’ll be doing in this phase is dividing the list of friends into a list of relatively good friends and a list of relatively bad friends. In order to do that we need to define a friend that’s in-between the two lists, called the pivot. This pivot is usually the first element of the list or an element picked randomly in the list. Friends preferred to the pivot will go into the first list, the others into the second list. In each list, we solve a subproblem that gets it sorted. Merging will become very easy as it will simply consist in appending the second list to the first one.
The subproblem is identical to the main problem… Obviously, if a list has only 1 or 2 elements, we don’t need to apply a quick sort to sort it… But in other cases, we can use the quick sort for the subproblems! That means that we will apply a quick sort to our two lists, which will sort them.
Yes, we can, because we use it for a strictly simpler problem, and if the problem is already too simple (that is, we’re trying to sort a list of 1 or 2 elements), we don’t use the algorithm. Let’s apply the quick sort on Sheldon’s example if we only consider his close friends.
Yes that’s what I’m saying. Let’s do a little bit of math to prove that. Suppose we have $n$ friends to sort. Denote $T(n)$ the number of operations to perform the quick sort. The dividing phase takes $n$ operations. Once divided, we get two equally smaller problems. Solving one of them corresponds to sorting $n/2$ friends with the quick sort, which takes $T(n/2)$. Solving the two of them therefore takes twice as long, that is $2T(n/2)$. The merging phase can be done very quickly with only 1 operation. That’s why, we have the relation $T(n) = 2T(n/2)+n+1$. Solving this equation leads you to approximate $T(n)$ by $n \log(n)/\log(2)$. For great values of $n$, this number is much much less than $n^2/2$.
In Sheldon’s example in which he has 212 friends, the number of operations required by the quick sort is about 1,600, which is much less than the 22 thousand operations required by the selection sort! And if you’re not impressed yet, imagine the problem Google faces when sorting 500 billion web pages. Using a selection sort for that would take millions of years…
Yes I did. It can be shown that by picking the pivot randomly, then in means, the complexity will be nearly the one we wrote. We talk about average complexity. But in the worst case, the complexity is not as good. In fact, the worst case complexity for the quick sort is the same as for the selection sort: it is quadratic. That’s why I prefer the merge sort who, by making sure the two subproblems will be equally small, makes sure that the complexity is always about $n \log n$, even in the worst case.
The reason why I wanted to talk about the quick sort is to show the importance of randomness in the algorithm. If we used the first element as pivot, then sorting a sorted list would be the worst case. Yet, it will probably happen quite often… Randomness enables to obtain a good complexity even for that case. Read more on randomness with my article on probabilistic algorithms!
P = NC?
The problem $P=NC$ is definitely a less-known problem but I actually find it just as crucial as the $P=NP$ problem (see my article on P=NP). Obviously if both were proven right, then $P=NC=NP$, which means that complicated problems could be solved… almost instantaneously. I really like the $P=NC$ problem as it highlights an important new way of thinking that needs to be applied in every field: parallelization.
The term parallel here is actually opposed to sequential. It is also known as distributed. For instance, suppose you want to compare the prices of milk, lettuce and beer in shops of New York City. You could go into each store, check the price and get out, but, as you probably know, NYC is a big city and this could take you months, if not years. What Brian Lehrer did on WNYC is applying the concept of parallelization on the comparing prices in NYC shops problem: he asked his auditors to check the prices as he opened a web page to gather the information. In matter of days the problem was solved. Check out the obtained map.
It surely does! The concept of divide and conquer was already extremely powerful in the case of a sequential algorithm, so I’ll let you imagine how well it performs in the case of parallelized algorithms.
You’re right! In a parallelized algorithm, you can run subproblems on different computers simultaneously. It’s kind of like task sharing in a company…
Except that there are no problems of egos with computers! Parallelization is a very important concept as more and more computers enable it. As a matter of fact, your computer (or even your phone) probably has a duo core or a quad core processor, which means that algorithms can be parallelized into 2 or 4 subproblems that run simultaneously. But that’s just the tip of the iceberg! Many algorithms now run in cloud computing, which means that applications are running on several servers at the same time. The number of subproblems you can run is now simply enormous, and it will keep increasing.
Parallelization is now a very important way of thinking, because we now have the tools to actually do it. And to do it well.
Almost. $NC$, which corresponds to Nick’s class after Nick Pippenger, is the set of decision problems that can be solved using a polynomial number of processors in a polylogarithmic time, that is with less than $(\log n)^k$ transitions, where $k$ is a constant, and $n$ is the size of the input. That means that parallelization would enable to solve NC problems very very quickly. In matters of seconds if not less, even for extremely large inputs.
$P$ stands for Polynomial. It’s the set of decision problems that can be solved in a polynomial time with a sequential algorithm. I won’t be dwelling to much on these definitions, you can read my future article on $P=NP$ to have better definitions.
As any parallelized problem can be sequenced by solving parallelized subproblems sequentially, it can be easily proved that any $NC$ problem is a $P$ problem. The big question is proving whether a $P$ problem is necessarily a $NC$ problem or not. If $P=NC$, then that means that any problem that we can solve with a single machine in reasonable time can now be solved almost instantaneously with cloud computing. Applications in plenty of fields would be extraordinary. But if $P \neq NC$, which is, according to Wikipedia, what scientists seem to suspect, that means that some problems are intrinsically not parallelizable.
Yes we do, just like we have the concept of NP-completeness to prove $P=NP$! There are a few problems that have been proved to be P-complete, that is, problems that are harder than other $P$ problems. If one of them is proven $NC$, then any other $P$ problems will be $NC$. Proving that a P-complete problem is $NC$ would solve the problem $P=NC$. One of these problems is the decision problem associated to the very classical linear programming problem. This problem is particularly interesting because it has a lot of applications (and there would an awful lot of applications if it could be parallelized!). Read my article on linear programming to learn about it!
I guess so… Still, a few problems sequentially polynomial have been parallelized and can now be solved much more quickly. For instance, let’s get back to sort algorithms. In the two divide and conquer algorithms we have described, subproblems are generated and can easily be parallelized. The number of subproblems cannot be more than the size of the list. It is therefore polynomial in the size of the list at any time. In the case of nearly equal subproblems, the number of iterations is about the logarithm of the size of the list. Therefore the parallelized sort algorithms is parallelized on a polynomial number of processors and has an almost polylogarithmic time. The only problem is the complexity time of the merging phase for the merge sort, and of the dividing phase for the quick sort.
However, those two difficulties have been overcome. In 1988, Richard Cole found a smart way to parallelize the merging phase of the merge sort. In 1991, David Powers used implicite partitions to parallelize the dividing phase for the quick sort. In both cases, this led to a logarithmic complexity. With huge datacenters, google can now perform sorting of web pages in matters of seconds. Impressive, right?
Let’s sum up
Computer science has already totally changed the world. For the new generation that includes myself, it’s hard to imagine how people used to live without computers, how they wrote reports or seek for information. Yet, this is only the beginning and parallelization will change the world in a way I probably can’t imagine. The advice I’d give you is to think with parallelization. It’s powerful concepts that need to be applied in various fields, including in company strategies.
In fact, I have applied divide and conquer by choosing the apparent lack of structure of the articles for Science4All. Classical structures would have involved a tree structure with categories of articles and subcategories, probably by themes of fields. But I’m betting on a more horizontal structure, where the structure is created by the links between the articles, via related articles or via authors.