A Mathematical Guide to Selling

I am not always excited by seminars I get to attend. But a few weeks ago, one seminar got me very excited. The presenter, Yang Cai, had solved the auction design problem. That’s the problem of how best to sell. Here’s one funny illustration of this selling problem:

In this article, I will not dwell on the solution by Cai and his co-authors — because their result is in fact more general than the auction design problem, and I’ll write about it in another article! Instead, I’ll tell you about what I knew before I listened to his talk and read his papers. As you’ll see, it was already pretty cool. But a bit frustrating…

The Auction Design Problem

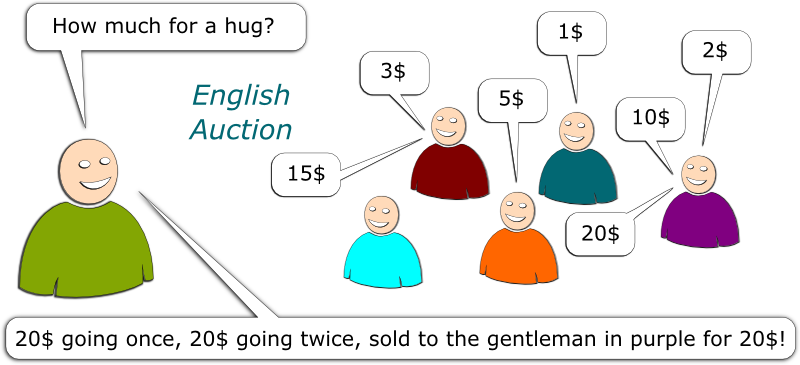
Let’s start with the example of the video. After all, it’s the most classic of all auctions. It’s the one you were probably thinking about when I told you about the auction design problem. It’s sometimes called the English auction.

How does it work, again?

Let me tell you about the auction design problem first. Imagine that a seller has one good to sell to potential buyers. As the commercial above exemplified it, the does not need to be material. It can be a help to jump out of a building more safely, or rights to operate some frequencies for telecommunication, or to have your ad displayed on a very visible platform. I’m mentioning these latter two, because they are literary billion dollar auctions — Google wins around 96% of his money through auctions via Adwords. When billions of dollars are at play, you can imagine that your auction design needs to be optimized.

I see! But how can auctions even be optimized? What’s wrong with the English auction?

I guess I should answer your first question now.

Oh yeah, that’s right. What’s the English auction?

In the English auction, a good is set at a certain low price. Potential buyers then bid higher and higher prices. The last bidder, who is also the one with the highest bid, then wins the good, and pays it at the price of his highest bid. It’s the one you see in many painting auctions and in many movies. You know? With the famous: “200 dollars going once, 200 dollars going twice, sold!”

Yes I see. So, what’s wrong with that auction?

The English auction is not that bad. Eventually, the good will be sold to the buyer that values it the most. But to get it, he’ll only need to bid slightly more than the highest bid of other potential buyers. Thus, the buyer will not sell it at the highest price you could possibly dream of, that is, the price at which the buyer actually values the good.

I see the problem. But is it possible to sell it at this highest possible price?

Sure, just sell the good at the price at which the highest bidder values it!

But I don’t know what that price is, do I?

You’re perfectly right! In fact, that’s precisely the difficulty of the auction design problem. To best sell, the seller needs some information that only the (highest) bidders possess. Yet, these bidders have all the incentives in the world not to reveal it to you — when you’re buying a car, do not tell the seller how much you’re really willing to pay to buy it! Instead, the bidders will do whatever they can to get the good, while paying it as cheaply as possible and definitely not more than how much they value the good.

I see… So we need to anticipate the bidders’ strategies when we design auctions, right?

Exactly! Now, let’s see what these strategies are in different simple auctions.

I’m using here the vague common definition of the term “strategies”, which I hope will help you have a good intuition of auction design theory. However, the vague notion of “strategies” here does not coincide with the formal mathematical definition used in game theory. In game theory, a strategy is just a thinking process that leads to a decision. Thus, a strategy can be naive, bad or optimal. But the concept of optimality of strategies is in fact very tricky, as one’s optimal strategy is only optimal with respect to others’ strategies. In fact, Nash’s brilliant insight was to involve a fixed point argument: if all bidders choose strategies that are optimal with respect to other bidders’ chosen strategies, then Nash talks about an equilibrium. For the sake of explanation, I won’t get into these (important) details, but I invite you to find out more with my article on game theory and the Nash equilibrium.

Example of Auctions

One trouble of the English auction is that it can be pretty long. Plus, the crowd of buyer needs to be quite calm, so that the seller can hear the bids. Yet, that was not the case during the epic tulip financial bubble.

Wait… What’s the tulip financial bubble?

It’s the first financial bubble in History! Back in the 1600s in the Netherlands, where banking was invented, the recent importation of tulips quickly became hugely popular. The demand was huge, but the supply was not — growing a tulip takes at least 7 years and nobody wanted to wait. The laws of economics tell us that this leads to the increase of prices. But then, because the prices of tulips were clearly increasing, traders knew they’d better buy a lot today, so that they can sell tomorrow at greater prices. This led to a boom of prices. At some point, a tulip would cost as much as a mansion! This is what’s nicely told in this cool video by Radar:

But as prices would increase every day, how then could sellers determine the prices of their goods, when they were permanently surrounded by noisy undisciplined crowds? The sellers’ preferred solution was the now-called Dutch auction.

How does it work?

The seller would start by a very high price. He would then decrease it until someone claims it.

So what are the bidders’ incentives in the Dutch auction?

It’s the great question! A trade-off appears for the bidder when the price is less or equal to what he’s willing to pay to get the good: If he waits, he can get it for a smaller price, but there’s a risk that another bidder would take it away from him. So, there is an information problem. Exactly like in a (first-price) sealed auction.

What’s the sealed auction?

It’s the one that had Joey Tribbiani unwilling buying a boat, on the classic TV show friends:

In the sealed auction, bidders secretly write down how much they’re willing to pay to get the good. The highest bid then wins it, like in the English auction.

Why did you say that the sealed auction was like the Dutch auction? I don’t see it.

In both case, the bidders’ rational strategy is to bid the smallest price that will secure the good, if the bidder is himself willing to pay that price. If a bidder knew all other bidders’ valuations of the good, this smallest price would equal the highest of others’ valuations (plus slightly more). Interestingly, this outcome is exactly the same as the one achieved by the English auction: The good is eventually assigned to the bidder that values it the most at the price of the second highest bidder.

What if bidders don’t know about other bidders’ valuations of the good? That’s the more realistic case, isn’t it?

You’re perfectly right. It’s a bit trickier though, so I’ll get there in a bit! For now, I want to mention one last auction: the Japanese auction.

What’s the Japanese auction?

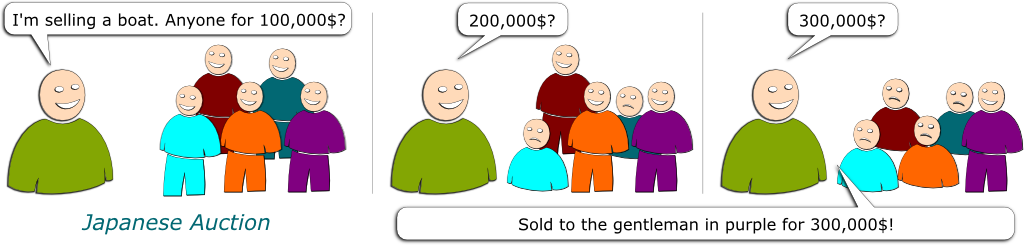
The Japanese auction is a bit of the converse of the Dutch auction, and is pretty similar to the English auction. The seller starts at a low price and slowly increases it. Bidders stand up and only sit down once they are unwilling to buy the good at the current displayed price. The good is eventually sold to the (literally) last man standing.

And this case, the bidders’ rational strategy is…

I guess it is to remain standing until the price exceeds the value they attribute to the good.

Exactly! In this Japanese auction, the bidders’ rational strategy is also the one we sort of expect them to play. In other words, the Japanese auction is incentive-compatible, in the sense that we give bidders incentives to bid the way we want them to bid.

The VCG Mechanism

The first person to really theorize auctions was the American economist William Vickrey. This would win him a Nobel prize in 1996. He noticed that all known auctions boiled down, as we’ve seen, to the good being sold to the highest bidder at the price of the second highest bidder’s valuation. So, he figured out, why not do directly a sealed second-price auction?

What do you mean?

Just like in the first-price sealed auction I mentioned above, we’re going to ask potential buyers to write down how much they’re willing to pay for the good. Still like in the first-price auction, the good will be sold to the highest bidder. However, this highest bidder will not have to pay the price he bid; he will have to pay the price that the second highest bidder bid.

OK… Is that any better than, say, the first-price auction?

The advantage of the sealed second-price auction is that it is incentive-compatible. In other words, bidders now have incentives to bid truthfully, that is, writing down how much they’re really willing to pay their good.

But it won’t earn the seller more money, will it?

No, it won’t. Once again, the outcome will be basically the same as in other auctions: The good will go to the highest bidder at the price of the second highest bidder. And that’s not so bad. At least, the good will go to the person that values it the most. In economist terms, the allocation is said to be socially efficient.

Well, it wasn’t hard to guarantee, was it?

In the case of the auction of a single good, indeed it was not — the English and Japanese auctions do that very well too. But let’s imagine another more complicated kind of auction. Imagine the government wants to construct roads connecting diverse cities, and he wants cities to pay for the roads.

Is that even an auction?

Yes! The outcome of the auction is a choice of road network, and the potential buyers are the different cities. Each city prefers some road networks to others, but will want to pay as little as possible as well. Pricing such a road network becomes much more complicated, as all cities benefit from the road network and it seems that they should thus all pay for it. But some cities will gain more from a certain road network than from another.

Wow! That auction looks pretty complicated…

It is. It’s really not clear how to best design it. Fortunately, the power of mathematics and the genius of Edward Clarke first and of Theodore Groves later have allowed a surprisingly elegant generalization of Vickrey’s auction to this more complicated general case, which we now call the Vicrkey-Clarke-Groves auction, or VCG mechanism.

So, how does the VCG auction work?

First, we ask each city to reveal how much it values the different road networks.

At this point, I really have to admit it: utility functions in all the auction design literature are assumed to be quasi-linear. This means that they must be written $u_i = v_i(x) – p_i$, where $x$ is the outcome (like getting the good or not) and $p_i$ is bidder $i$’s payment. In particular, this means that bidders are assumed to be risk-neutral. Yes, that is a big unrealistic assumption. But, as I’ll tell you in a future article, Cai and his collaborators have successfully faced the more general case where this assumption is not necessary!

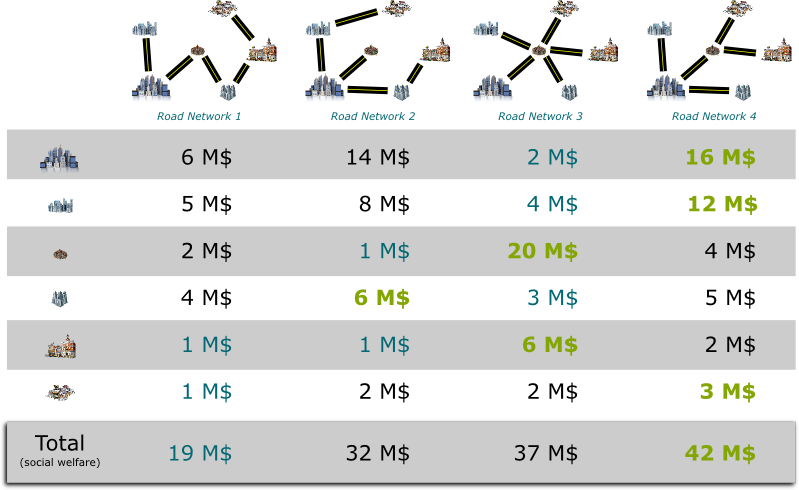
We then choose to build the road network that the cities altogether value the most: The fourth road network.

Note that we cannot stop here! We must have cities paying, otherwise the auction would not be incentive-compatible. The cities’ strategies would consist of largely overbidding the road networks they do like and largely underbidding the road networks they do not like, hence the bids we receive would be meaningless, and we would be able to determine the road network that maximizes social welfare.

But how much are cities going to pay for it?

That’s the big question. Clarke’s brilliant answer was to have cities paying their negative externalities on the collectivity.

What do you mean?

Consider one city called NYC. If it was not there, his bids would not be considered, and thus, the road network chosen by the VCG auction might be different. But if it is different, it means that other cities would be happier without NYC. How much happier they would be is exactly what NYC must pay, according to Clarke.

As you can see in the figure, if the big city was not there, then road network number 3 would have been chosen, as opposed to road network number 4. The value of road network 3 for the other cities would be 35 million dollars, as opposed to the 26 million dollars of the road network number 4 that has been chosen, because of the city’s presence in the auction. Therefore, the negative externality of the big city is 35-26 = 9 million dollars.

I see… And is that what the big city will have to pay?

Yes indeed! Similarly, the second largest city will have to pay 3 million dollars. Conversely though, other cities do not have to pay anything, as their presence has had no effect on the choice of the road network. Indeed, were other cities not there, the auction would still have decided to go with road network number 4.

I see. So the VCG auction has collected 12 million dollars. Is that enough to build the road?

I don’t know. The trouble of VCG is that it hardly controls how payments will be made. Its main advantage is to be an (dominant-strategy) incentive-compatible mechanism that guarantees the choice of the socially efficient outcome. So, if you’re a state and want to guarantee the happiness of the people, VCG is the way to go. But if you have also monetary considerations in mind, it may not be that good.

In such a case, what else can we do?

The VCG auction is actually the particular case studied by Clarke of the more general class of Groves mechanisms. Crucially, all Groves mechanisms are still incentive-compatible and socially efficient, but they yield different payments. The key of it all lies in the fact that one’s payment depends in a very specific way on what one bids. What’s good about the VCG auction in particular is that the auction designer never has to give money to any bidder, and that bidders are all happier after the auction (given outcome and payments) than before — this is called individual rationality.

I know you’re dying to see the maths, so here it is! Let’s denote $v_i(x)$ the bid of bidder $i$ for outcome $x$. Bidder $i$’s payment must be of the form $h_i(v_{-i}) – \sum_{j \neq i} v_j(VCG(v))$, where $VCG(v)$ denotes the socially efficient outcome chosen by VCG and $h_i$ any function of the bids of all bidders but $i$. Crucially, this payment depends on $v_i$ only in the determination of the outcome $VCG(v)$. In fact, the happier others are with the outcome $VCG(v)$, the less bidder $i$ will have to pay. In the end, the way bidder $i$’s bid will affect his utility is exactly through the outcome chosen by VCG, and more precisely, through the sum of his utility $v_i(VCG(v))$ and others’ utilities for this outcome $\sum v_{-i}(VCG(v))$. In fact, to maximize his utility, bidder $i$ will exactly want to reveal his bids in such a way that the VCG auction will manage to output the social efficient outcome $VCG$. And since VCG wants social efficiency, bidder $i$ can make sure it will succeed by revealing his true valuation function $v_i$. We’ve just proved dominant-strategy incentive-compatibility! As an exercise, I’ll let you prove the other properties of VCG I mentioned, the fact that it generalizes the Vickrey auction and that VCG is a particular case of Groves mechanisms.

Myerson (1981)

The VCG auction is pretty impressive. But, as a seller, it may be of little interest to you. You may not care about social efficiency. You may prefer money. This is called the revenue-optimization auction design problem. And its study turned out to be an even greater mathematical challenge! While the VCG auction was fully determined in the early 1970s, it was only in 1981 that the giant of mathematical economics, Roger Myerson, would solve the revenue-optimization auction design problem in the case of auctions of a single good. In fact, Myerson’s seminal 1981 paper is what won him the Nobel prize in economics!

Is revenue optimization so much harder?

It really is! In fact, it’s too complicated for me to tell you about the details of Myerson’s many insightful theorems. I’ll only tell you about his two most important theorems. The first is an astounding result. It is called the revenue equivalence theorem.

What’s the revenue equivalence theorem?

Roughly, it asserts that the seller’s expected revenue is fully determined by the allocation rule of the good. In particular, all the auctions we’ve discussed so far all end up giving the good to the person who values it the most. Thus, they all have the same allocation rule. Therefore, thanks to Myerson’s revenue equivalence theorem, we can assert that they are all revenue-equivalent.

That’s very counter-intuitive! I thought that the first-price auction would earn the seller more money than the second-price auction!

I know it would seem so. Even weirder, some bizarre auctions, like the all-pay auction where bidders need to pay their bids no matter what, are revenue-equivalent to the English auction! Personally, I was deeply surprised by Myerson’s result — and still kind of am!

So where does the revenue-equivalence theorem come from?

It lies in the features of the Bayesian setting, and, more specifically, in the necessary properties of so-called Bayesian-Nash equilibria in single-good auctions. It’s hard for me to give you a deep insight into what’s going on here, but roughly, the allocation rule and the Bayesian-Nash equilibrium condition (plus individual rationality) leave no choice for the expected payments of the different bidders.

The key to understand Myerson’s revenue-equivalence theorem is to think in terms of so-called ex-interim allocation and payment rules (which I like to call the return functions). Given one’s bid, these output the probability of getting the good and the expected payment. You’ll notice that incentive-compatibility implies that, first, the ex-interim allocation rule must be nondecreasing, and then, that the ex-interim payment rule must be written as a function of the ex-interim allocation rule and its primitive (there’ll be one constant which should be adjusted to 0 to guarantee individual rationality). Assume in addition that the strategy is onto (all bids can occur), the properties of ex-interim allocation and payment rules are not only necessary but also sufficient to guarantee incentive-compatibility.

Now, if Myerson had only proved the revenue-equivalence theorem, then he’d probably still have won the Nobel prize. But he did more, in this very same article. He also determined the revenue-optimal auction.

Wait a minute… Is there really a way to do better than all the auctions you’ve told us about?

There is! And the key is not to necessarily sell the good to the person who values it the most, as opposed to what’s done in all classical auctions! In fact, Myerson proved that, in some cases, it’s better not to sell!

What? Why? Aren’t you getting zero instead of something by not selling?

I know. Once again, that’s very counter-intuitive. Here’s one way to understand this. The seller needs leverage. Otherwise, bidders would take advantage of the seller’s sell-at-all-price behaviour, and will succeed in lowering the price. To get this leverage, the seller needs to firmly tell bidders that there are prices under which he will not sell. This threshold price is what Myerson called the reserve price. Of course, it may then be that the reserve price exceeds the bidders’ actual valuations of the good. In such a case, it is essential that the seller commits to not selling the good — incentive-compatibility relies on it! Thereby, he might lose an opportunity once in a while, but, crucially, in the long run, he will earn more.

So how much should this reserve price be?

It depends on the seller’s belief of the bidders’ valuations. Very roughly, if the seller believes that bidders have high valuations, he should set a high reserve price accordingly.

Mathematically, this belief should be expressed as a probability density function $f$ over bidders’ possible valuations. Denoting $F$ the cumulative distribution function, the reserve price is the value $v$ such that $v f(v) = 1-F(v)$.

Is that why tourists always get overpriced?

Exactly! So keep that in mind the next time you’ll get offended by local sellers’s poor treatments of you as a tourist. They’re not being xenophobe; they’re just being smart!

The example in the cartoon above is exactly Myerson’s auction for a single good with a single bidder.

So is that it? Is Myerson’s auction simply about adding reserve prices?

In the case where all bidders look the same to you, yes. But in the case where some bidders look more willing to pay than others, Myerson proved that you should use the threat of selling to other bidders to convince high bidders to bid their true valuations of the good. And this means that you should commit yourself to not necessarily sell the good to the bidder who values it the most!

More precisely, denoting $f_i$ and $F_i$ the probability density and cumulative distribution functions of the seller’s belief on bidder $i$’s valuation of the good, and given bidder $i$’s bid $v_i$, Myerson’s auction requires to compute the virtual valuation $\psi_i(v_i) = v_i – (1-F_i(v_i))/f(v_i)$. The good is then sold to the bidder with the highest virtual valuation, if this highest virtual valuation is nonnegative.

That does not sound very ethical…

It’s an interesting point. Indeed, Myerson’s optimal auction is not anonymous, in the sense that not all bidders are treated in the same way. In fact, any careful study of Bayesian theory would tell us that this is quite often the case: Optimal decisions discriminate based on beliefs (or, as some people like to call them, on prejudices). In Myerson’s auction case though, it might make you feel better that it advantages bidders who seem less willing to pay a lot for a good, who are likely to be poorer than the others…

Wait! What about the pricing rule?

Don’t you remember? Myerson’s revenue-equivalence theorem says that it doesn’t matter! Any auction that allocates the good exactly as Myerson’s optimal auction does will win the seller the same amount of money (in the long run).

Let’s Conclude

Unfortunately, Myerson’s optimal auction has two clear limits. First, he assumes that bidders are risk-averse. In particular, they only care about the expected gains. But, by talking to people on the streets, Derek Müller found out that this was clearly not the case, as we can see it in this Veritasium video:

Myerson’s optimal auction isn’t the only one that requires bidders’ risk-aversion to guarantee incentive-compatibility. The VCG auction also strongly relies on this assumption.

But, more importantly, it only deals with single-good auction. That’s very restrictive, and, naturally, economists and mathematicians all wanted to build upon Myerson’s work to address the multi-item auction case. Well, guess what: For over three decades, no one would manage to succeed! Up until a month ago, I thought that it was hopeless. I didn’t even dare to try.

But…

But to my great surprise, Yang Cai and his co-authors proved me wrong! In a series of three 2012-2013 papers (75 pages!), using powerful technics from computer science, they solved in the largest possible sense the auction design problem! I got terribly excited when I read their proof… And that’s what I’ll discuss in a future article! Stay tuned (for instance by subscribing!).