The Addictive Mathematics of the 2048 Tile Game

I did it! After weeks of alienating efforts, I did it. I made it to the end of the 2048 tile game.

It’s the Internet sensation of these days. It’s a game played on 4×4 grid, with numbered tiles. At each stage, you slide tiles in any of the four directions of the screen (up, down, left and right). If two tiles of the same number fall onto one another, then they merge into a tile whose number is the sum of the tiles’ numbers. Once tiles have slid and merged, a new tile pops up at a random free location of the grid. With 10% chance, it’ll be numbered 4. Otherwise, it’ll be numbered 2.

The best way to get them is to actually play the game. That’s why, if you’ve never played the game, I invite you to spend some time playing it right now (but try to stop before becoming completely addicted to it!).

In its basic version, the game stops as soon as you manage to create a 2048 tile. But, as a nerdy mathematician, it sounds way too arbitrary to me. So, I tried to go as far as I could. And, a few days ago, after weeks of effort, I did it! I’ve reached the mathematical end of the game that’s displayed on the right! This means that, even in principle, you cannot go further than this.

The game raised numerous intriguing questions about the underlying mathematics of the game. From induction to isomorphisms, including geometric sums, topology, probability and optimization, these mathematical questions are these I address in this article!

Powers of 2

Let’s start with the simple observation that all tiles are powers of 2.

What seems obvious still needs to be proved in mathematics! And your repeated observations that all the configurations you’ve ever seen only contain powers of 2 have little mathematical bearing. We’re not doing physics here!

A simple proof is by mathematical induction. More precisely, we’ll show that at any stage of the game, all tiles are powers of 2.

To prove that all tiles are powers of 2 by mathematical induction, it suffices to prove two simpler points:

1. At first, all tiles are powers of 2.
2. Assuming that, at some stage, all tiles are powers of 2, then, at the next stage, all tiles will still be powers of 2.

Point 1 fact is pretty straightforward. Indeed, at first, the only tile on the grid is the initial 2s or 4s we start with. And, as we all know it, 2 and 4 are powers of 2. More precisely, we have $2 = 2^1$ and $4 = 2^2$.

In point 2, we assume that at a given stage, all tiles are powers of 2. We need to show that no matter which move we then do, all tiles will still be powers of 2. The key to show that is to notice that all tiles that can be created in a move are either the randomly generated new tile or a tile obtained by combining two identical tiles. Yet, in the first case, we have see that tiles randomly generated are either 2 or 4 which are both powers of 2.

In the second case, the number of the newly generated tile is the sum of two identical tiles of the previous stage. Yet, we assumed that all tiles of the previous stage were powers of 2 (this is known as the recursion hypothesis). Thus, the two identical tiles that were added are of the form $2^k$ for some whole number $k$. Then, the number of the new tile equals $2^k + 2^k$. A bit of algebra then implies that $2^k + 2^k $=$ 2 \times (2^k) $=$ 2^{k+1}$… which is still a power of 2! What we’ve shown is that, assuming all existing tiles were powers of 2, any new tile obtained by combining existing tiles will still be a power of 2: This was the second case we needed to in our proof by mathematical induction.

Then, by mathematical induction, the proofs of the two points imply what we’ve wanted to prove all along. Namely, we now have a complete proof that all tiles are always powers of 2.

Geometric Sums

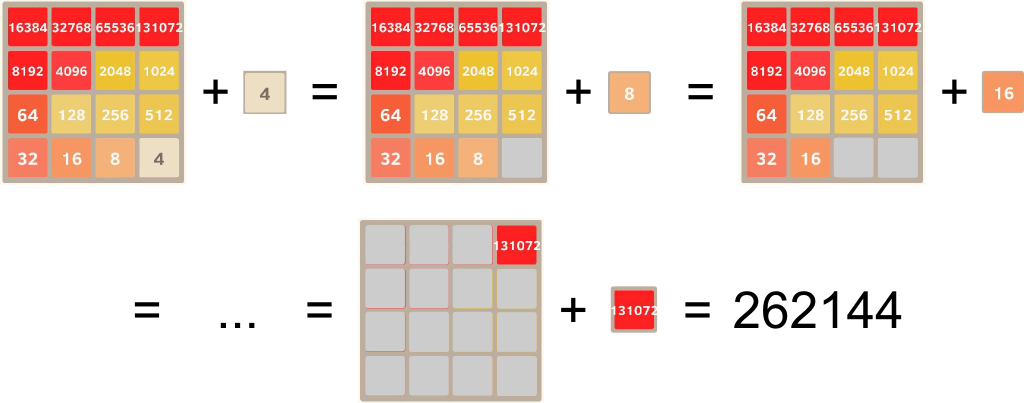
Let’s now discuss the mathematical end of the game. In the introduction, I claimed that the configuration I reached couldn’t be surpassed. But before getting there, let me compute the sum of all tiles of that configuration.

As a lazy mathematician, I don’t like doing long additions… So let me show you a trick to easily compute the sum of this all.

Let me add $4$ to the sum $4+8+16$+$…+131,072$. By combining 4 with our tile 4, we obtain a new tile 8. But then, this new tile 8 can be combined with the existing tile 8, hence creating a new tile 16… And so on.

Amazingly, our computation simplifies to the simple addition $131,072+131,072$. Now, don’t forget that we had to add $4$ to $4+8+16$+$…+131,072$ to obtain that number. So to determine $4+8+16$+$…+131,072$, we merely need to subtract 4 to the computation we did above, hence obtaining $4+8+16$+$…+131,072 $=$ (131,072 + 131,072) $-$4 $=$ 262,140$. How awesome is that?

It’s the magic of so-called geometric sums. Our geometric sum is $2^2+2^3+2^4$+$…+2^{17}$, and we have the crucial property $2^k + 2^k $=$ 2^{k+1}$. So, by adding $2^2$, we have

$$\begin{array}{rccll}
&2^2 &+& (2^2+&2^3+2^4+… +2^{17}) \\
=& (2^2+2^2) &+& (&2^3+2^4+… +2^{17}) \\
=& 2^3 &+& (&2^3 + 2^4 +… + 2^{17}).
\end{array}$$

You can see a pattern appearing, which hints at $2^2 $+$ (2^2+2^3+2^4$+$…+2^{17}) $=$ 2^k $+$ (2^k + 2^{k+1} $+$ … + 2^{17})$. As it turns out, you can prove (still by induction!) that this pattern really holds for all $k$. For $k=17$, we finally get $2^{17}+2^{17} $=$ 2 \times 2^{17} $=$ 2^{18}$. Hence, $2^2$+$(2^2+2^3+2^4$+$…+2^{17}) $=$ 2^{18}$, or, equivalently, $2^2+2^3+2^4$+$…+2^{17} $=$ 2^{18} – 2^2$.

In fact, the pattern is so strong that it can be generalized for powers of 3, powers of 4, or in total generality, for powers of any complex number $q$ (or, even, any element of a unitary ring!). The magic of geometric sums then yields $(q^k+q^{k+1}+… $+$q^n) \times (q-1) $=$ q^{n+1} – q^k$, for all whole numbers $k \geq n$.

The Mathematical End of the Game

Now, to prove that the configuration of the introduction is the mathematical end of the game, it suffices to show that the sum of tiles reaches its maximum in the configuration I got. In other words, let’s show that tiles cannot add up to more than $2^{18}-2^2 = 262,140$.

Notice that, after every move, the total sum of tile numbers increases by the number of the new randomly-generated tile. This new tile is either 2 or 4. So, the total sum of tile numbers increases by steps of 2 or 4. So, to get to a configuration whose total sum of tile numbers is more than $262,140$, one must have gone through $262,140$ or $262,142$. But, as we shall prove it, $262,140$ is necessarily an end game configuration and $262,142$ is unreachable.

It all has to do with the decompositions of these numbers as sums of powers of 2. To have the tiles fitting in the bounded 4×4 grid, we need to find decomposition as efficient as possible, in the sense that we want to write the sum of tile numbers with the smallest possible number of powers of 2.

It’s easy to see that, in any most efficient decomposition, powers of 2 must appear only once. Indeed, otherwise, we can just combine 2 identical powers of 2 into their sum, hence yielding the same sum with one less tile.

Let’s take $262,140$ for instance. A simple test shows that $262,140$ is not divisible by $8$. Yet, all powers of 2 greater or equal to $8$ are multiples of $8$. Thus, a sum of powers of 2 that equal $262,140$ must contain a power of 2 smaller than $8$. So, there must be tiles $2$ or $4$. But do we have one tile of 2 and one tile of 4? Or just one tile of 2? Or just one tile of 4?

Notice that, once tiles of 2 and 4 subtracted, we need to obtain a multiple of $8$. Among the three possible alternatives, only the the last case with only the tile of 4 can guarantee that this is the case. So, in the most efficient decomposition of $262,140$, there’s no tile of 2 and one tile of 4. Meanwhile, the other tiles must then add up to $262,136$. Once again, noticing that $262,136$ is not divisible by 16 implies that the most efficient decomposition of this number contains one 8. And so on…

Exactly! In fact, the most efficient decomposition of $262,140$ is precisely the one of the introduction! Yet, this decomposition is made of 16 different powers of 2. Thus, no two tiles can be combined. And, since there is no more room on the grid, no move can be done. It is thus necessarily an end configuration!

The most efficient decomposition of $262,142$ is $262,142 $=$ 2^1 + 2^2+2^3 $+$ … +2^{17}$, which contains 17 terms. This cannot fit in the 4×4 grid. Thus, $262,142$ is mathematically unreachable! This concludes our proof that the configuration of our introduction is the mathematical end of our game.

The Probability of Getting There

Some of my friends pointed out that I was in practice mode with unlimited undos, and have pointed out that this is sort of cheating. Or, at least, this is making the game much much easier. It does. To the point that it is also mathematically impossible to get to the end configuration in the normal mode with 5 undos.

Well, nearly. What I’ll claim is that within our lifetime, no human (nor computer!) can ever get there without unlimited undos. Or, at least, it is overwhelmingly unlikely for anyone to get there.

For a start, let me point out that $2^1+2^2+2^3+…+2^{16} $=$ 131,070$ is necessarily an end configuration of the game, since its most efficient decomposition is made of 16 different tiles. The argument we gave for $262,140$ being the end game also holds here. So we must never go through $131,070$ if we want to go beyond this number.

First, we must have gone through $131,068$ and we must be lucky enough so that the randomly generated tile at this stage is a 4, not a 2. This means that we have at most one chance out of 10 to jump over $131,070$.

Yes. But our argument for $131,070$ also holds for many more total sums of tiles. To see why, let’s notice that $131,070 $=$ (2^1+2^2+2^3$+$…+2^{16}+2^{17}) $-$ 2^{17}$. But our reasoning actually applies equally well to all numbers of the form $(2^1+2^2+2^3$+$…+2^{17}) $-$ 2^k$ for $k$ between 2 and 17 (the case where $k=1$ is actually our mathematical end of the game), as all these numbers require 16 powers of 2 to be decomposed into. Therefore, these 16 numbers need to be jumped over. Thus, 16 times during the game, we need to be lucky enough to have a 4 appearing, not a 2.

It does! This yields a probability of at most one out of $10^{16}$ to have a chance to get to the end configuration, had we zero undos. With 5 undos, we have 5 times more odds. But even then, the probability of a game being playable until the mathematical end is less than 1 out of $10^{15}$. And in fact, because we only looked at one possible impossibility of the game, the actual probability of a game being playable until the mathematical end is definitely much much smaller than that (this actual probability is extremely hard to compute though…)!

For sure, humans can’t. Even if every human played one game every day for 100 years, we couldn’t play about $10^{15}$ games!

If the actual probability of a game being playable to the mathematical end is probably overwhelmingly less than one out of $10^{15}$ (and I think it is), computers won’t have a chance either… In other words, it is hopeless to ever get to the mathematical end of the game in a non-practice mode.

Topology and Paths

So far, our discussions have mainly about the numbers underlying the game. We focused on what the tiles are. But any player of the game would notice that this is far from being the only thing that matters in the game. Something else is at least as important.

I’m hinting at the positions of the tiles. To go far in the game, tiles must be nicely ordered on the 4×4 grid. And this is a matter of topology.

Topology literally means the study of location.

There is a subtle, but crucial difference between topology and geometry. While geometry is concerned with actual shapes of objects, its angles and distances, topology is blind to these concepts. Instead, topology merely focuses on how the components of objects are connected. In our case, the components of our game are tiles, and it is important to see how they are connected to one another. In fact, if you look at the mathematical end of the game I’ve reached, you can see that there is a clear pattern in the way tiles are connected.

Yes. And that’s a crucial feature you want to have when you play this game! Indeed, for two tiles to be combined, they need to be close to one another. Technically, they need to be on the same row or the same column, with no tile in between. So, obviously, the best way to make sure that two tiles can be combined is to have them touching one another. Similarly, we’d better have tiles which are meant to be combined eventually near one another. This means that $2^{k-1}$ should be near $2^k$, especially when $k$ is so large that it’ll be hardly feasible to create another tile $2^{k-1}$.

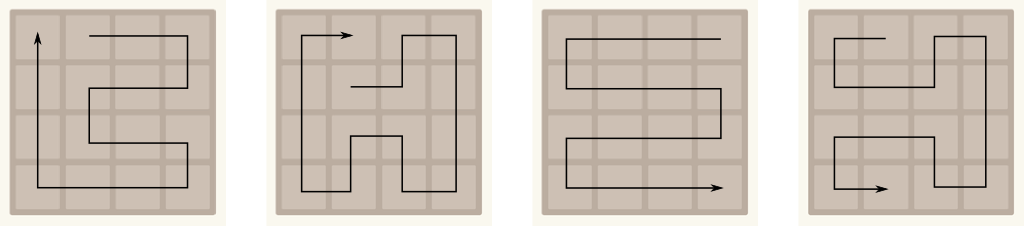
Exactly. So, eventually, we should have some sort of path from $2$ or $2^2$ to $2^k$ that goes through all powers of 2 in-between! In fact, it’s useful to imagine what sort of longest path we can aim at on the 4×4 grid. Below are some of alternatives:

Optimal Strategy

Now, in my experience, following the most stable of these paths is a great strategy. And the snake line seems quite stable.

What I mean is that we can maintain or get back to the snake line rather well despite the perturbation created by the randomly generated tiles. It’s a bit as if you driving a car and wind was blowing gusts left and right. Then, a flat large highway will be more stable than a tortuous mountain track.

Hummm… There’s a trouble here with the concept of “best” strategy. In fact, let’s listen to Steve Mould and James Grime discussing good strategies of the game:

So, importantly, there is uncertainty in the game. Namely, the randomly generated new tiles of each stage create an uncertain environment. In such uncertain environments, there are several possible concepts of optimality:

• Best-case optimality (this is unconventional…): The best strategy in the ideal case where randomly generated tiles always appear exactly where we’d like them too.
• Stochastic optimality (average): The strategy that works best in average.
• Robust optimality (worst-case): The best strategy that works in the worst case where randomly generated tiles always appear exactly where we wouldn’t like them to.

The best-case is basically the one I’ve been talking about so far. Whenever I didn’t like the location of the new generated tile, I just did undos until it was at a satisfying location. Now, since I got to the mathematical end of the game using the snake line strategy, I can guarantee that the snake line is a best-case optimal strategy!

It’s the one you should be using when playing according to the classical mode with limited undos. A stochastic optimal strategy should then ensure you the maximality of your average score at the end of the game. But, like often when it comes to stochastic optimization, determining the stochastic optimal strategy is very, very, very difficult.

Indeed. Quite often in optimization research, stochastic optimization is simply too hard to handle. The next best thing is then to turn towards robust optimization, which has been very successful in many applications. However, in our case, as hinted at by Steve Mould, robust optimization is probably way too conservative an approach. It makes sure that we can get far enough, but does not aim at going very far…

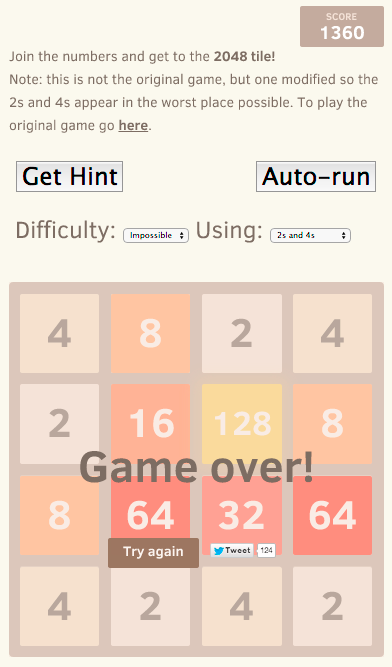
What I mean is that the worst-case imagined by robust optimization is in fact terribly unlikely that it is not relevant. It’s easy to get a feel for that! Try to play this version of the game, where the computer will always try to put you in this worst-case. As you’ll see, it’s a very different game that you’re suddenly playing! In fact, the best I’ve had in this version is the figure on the right…

Isomorphism

In my research lab where we often play card games, I’m kind of known for abusing of my favorite mathematical word: Isomorphism. How funny was it for me that James Grime used it just as I would:

Two games are said to be isomorphic if they are essentially the same. So for instance, if you replaced all classical tiles $2^k$ by exponent tiles $k$, then the game will be isomorphic to the classical games. The difference though, is that combining two exponential tiles $k$ would yield the exponential tile $k+1$ (which corresponds to combining two classical tiles $2^k$ into a tile $2^{k+1}$). While the numbers and the visual representations of the tiles would be different, the game would remain essentially the same. Any stage in one could be translated into a stage of another. Any strategy in one corresponds to a strategy in the other. Fundamental properties of one (like end game and optimality) are fundamental properties of the other. In mathematical terms, the games are isomorphic.

Yes. Conversely, while the hard version of the game where the computer plays against you has the same visual representations as the classical 2048 tile game, it is definitely not isomorphic to the classical game. In particular, any good strategy in the classical 2048 tile game doesn’t translate into a good strategy of the difficult version. Similarly, the Fibonacci version is not isomorphic to the classical 2048 game, as the new rules of tile combinations completely mess up topological considerations!

There are other underlying isomorphisms in this game. Namely, if we rotate the game by 90° all along, then the game is unchanged a priori. Similarly, albeit trickier, if we permute up and left while permuting down and right, then the game is still essentially the same. In particular, in the configuration on the right, all moves are isomorphic. You can either go up or left, and both moves are essentially the same.

It is! Symmetry is the geometrical word corresponding to the more fundamental concept of isomorphism. Two objects are symmetric if they are (geometrically) essentially the same.

Yes it will. But given that this next tile hasn’t appeared yet, and since our uncertainty about where it will appear respects the symmetry too, the two moves are in fact symmetric prior to when the next generated tile appears.

Let’s Conclude

The 2048 tile game raises plenty of interesting underlying mathematical questions. Maybe not as interesting as physics or chemistry according to some professors though…

With all due respects to these professors, I personally find the 2048 tile game very (too?) addictive. And it’s also mathematically intriguing, as a deep understanding of the game takes us through the concepts of induction, geometric sums, probability, combinatorics, topology, optimization, game theory and isomorphism we have discussed in this article. In fact, I find the game so puzzling that, I’ll admit it, I’ve already dreamt of it…