Dynamical systems such as a system of 3 planetary bodies can exhibit surprisingly complicated behavior. If the initial state of the system is slightly varied, the resulting system behaves in a radically different manner. This "sensitivity to initial conditions" is a key element of what's become (perhaps disproportionately) well-known as chaos. Using the mathematical notion of iterative systems, we can model such systems and understand how chaos arises out of deceptively simple foundations.

The study of dynamical systems, natural or abstract systems that evolve at each instance in time according to a specific rule, is an active and fruitful area of research in mathematics. Its study has yielded insights into the nature of social networks such as Facebook, the spread of diseases such as influenza, and the behavior of the financial markets. In this series of posts, we'll look in depth at dynamical systems, as well as at the related subjects of chaos theory and fractals, all of which are both interesting and useful for understanding our world.

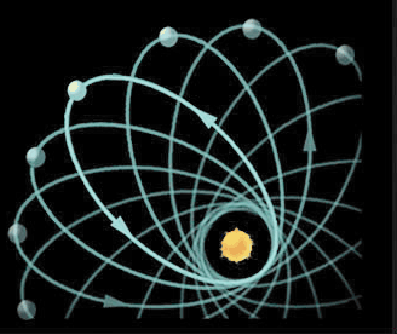
From our "intrinsic" point-of-view on the surface of the Earth, it appears to be flat, but if we examine the Earth from the "extrinsic" point of view, somewhere off the Earth's surface, we can see that it is clearly a curved surface. Amazingly, it is possible to determine that the Earth is spherical simply by taking measurements on its surface, and it is possible to generalize these measurements in order to study the shape of the universe. Mathematicians such as Riemann did just this, and Einstein was able to apply these geometric ideas to his "general theory of relativity", which describes the relation between gravitation, space, and time.

Geometry literally means "the measurement of the Earth", and more generally means the study of measurements of different kinds of space. Geometry on a flat surface, and geometry on the surface of a sphere, for example, are fundamentally different. A consequence of this disparity is the fact that it is impossible to create a perfectly accurate (flat) map of the Earth's (spherical) surface. Every map of the Earth necessarily has distortions. In this post we look at a few different methods of map-making and evaluate their distortions as well as their respective advantages.

This is the first of a series of three posts. In this post we'll see how the Greeks developed a system of geometry - literally "Earth measure" - to assist with planetary navigation. We then will see why their assumption that the Earth is flat means that Euclidean geometry is insufficient for studying the Earth. The Earth's spherical surface looks flat from our perspective, but is actually qualitatively different from a flat surface. In the ensuing posts, we'll see why this implies that it is impossible to make a perfectly accurate map of the Earth, and build on this idea to get a glimpse into Einstein's revolutionary theories regarding the geometry of the space-time universe.

Recent discoveries in the branch of physics known as quantum mechanics have powerful applications in the field of network security - they have the potential to break forms of internet security based on mathematics such as the RSA algorithm, and also present new ways to safely send information. In this article we’ll see how a physics-based method can be used to secure online information.

Over 300 years ago, a mathematician named Fermat discovered a subtle property about prime numbers. In the 1970's, three mathematicians at MIT showed that his discovery could be used to formulate a remarkably powerful method for encrypting information to be sent online. The RSA algorithm, as it is known, is used to secure ATM transactions, online business, banking, and even electronic voting. Surprisingly, it's not too difficult to understand, so let's see how it works.