The Biology Civil War Opposing Kin to Group Selection

In a workshop on biodiversity I’ve just attended, Matthijs van Veelen’s third slide listed today’s greatest biologists, separated in two columns. And there’s little doubt about one fact: One side is deeply wrong.

Conflicts had been there for long. But in August 2010, Martin Nowak, Corina Tarnita and Edward Wilson triggered the war, as they published a highly controversial article in Nature. This article harshly and violently criticizes the established and 40-year-old kin selection and inclusive fitness theory, and argues that group selection theory should be used instead. Yet, the anti-group selection team typically considers that “inclusive fitness is as general as the genetical theory of natural selection itself“.

There were! In fact, 137 biologists co-signed a response claiming that the arguments of the controversial article “are based upon a misunderstanding of evolutionary theory and a misrepresentation of the empirical literature“. Many other responses have followed like Richard Dawkin’s, who views the controversial article as a “public disgrace“. And the debate is still ongoing…

Well, after a thorough read through Nowak’s controversial article and the reactions it generated, I must say that I… You know what? Let me not tell you now and get you introduced to the nature of the debate first!

Kin Selection and Inclusive Fitness

Let’s start with kin selection theory. This theory was triggered by a 1964 seminal paper by William Donald Hamilton, who tried to put evolutionary biology on solid mathematical foundations. At this time, biologists were faced with one puzzling thought.

It’s the issue of the existence of altruism despite natural selection. Take the example of Belding’s ground squirrels. When in sight of a predator, a ground squirrel would give an alarm to warn his kin of the danger. By doing so though, the squirrel also reveals his location to the predator, hence endangering his life and lowering his chance of survival! Applying Darwin’s theory of evolution brutally would suggest that altruistic squirrels would eventually go extinct, in favor of their relatives who do not have such a behavior…

You’re right! Individuals don’t evolve. After all, individuals always die. But genes do.

Genes are the codes encrypted on DNAs that make up individuals. This code is what’s transmitted from generations to generations through reproductions. And, as opposed to individuals, genes can survive through time as they are carried out by descents. Richard Dawkin referred to these surviving genes as selfish genes. This is what’s explained by Eric Olson on Instant Egghead:

That’s where kin selection enters in play. Its essence is conveyed by the following famous quote by British evolutionary biologist John Burdon Sanderson Haldane, when he was asked whether he would sacrifice himself to save another person:

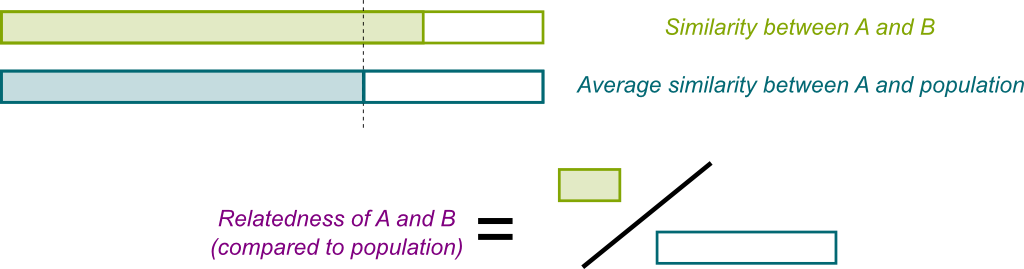
Crucially, your relatives share many more genes with you than with the rest of the population. Thus, by helping them reproduce, you’re also advantaging your genes! Now, your cousins’ genes are less similar to yours than your brothers’ are. So, it’s better for your gene survival that you save a brother rather than a cousin. More generally, the resemblance of your genes with others’ is a very concept captured by relatedness.

Hummm… This is where opinions start to diverge. As far as I can tell, all biologists would agree that there is no precise definition of relatedness! Still, let me give you the most usual one: Relatedness between individuals A and B is a measure between 0 and 1 of the gene similarities between A and B, compared to the gene similarities between A and the average of the population. In other words, relatedness is a normalization of gene similarities such that the relatedness between A and himself is 1, and such that its relatedness to the average of the population is zero. The following figure displays this.

The theory of inclusive fitness is then centered around Hamilton’s use of relatedness to derive what’s known as Hamilton’s rule. This rule says that the altruism of A for B is favored over the non-altruism, if the benefit to B multiplied by relatedness exceeds the cost to A.

Let’s define the variables more precisely. By helping B, A will be reducing his average number of kids. The average decrease of the number of his kids is A’s cost. On the opposite, individuals B who benefit from altruistic behaviors like A’s will increase their average number of its kids. This increase is its benefit. Finally, the average number of genes of A that B will be passing is precisely measured by the relatedness.

If A helps B, A will increase through B the presence of its genes to the next generation by the left term of the formula above. If this exceeds what A would have passed itself had it not helped B, then altruism will pass more genes to next generations than selfishness! Thus, altruism is favored if and only if Hamilton’s rule holds!

This argument is the core of kin selection and inclusive fitness theory. By opposition to fitness theory in which individuals only maximize the number of their offsprings, inclusive fitness theory is based on individuals maximizing the number of offsprings which have similar genes to the individuals! In essence, this corresponds to maximizing one’s offsprings and the sum of offsprings of others multiplied by relatedness.

Well, in fact, as far as I understand, all biologists agree that Hamilton’s rule doesn’t always hold in practice…

Hehe… Now we’re getting to the really interesting part!

Micro-Macro Transitions

In essence, the problem of our reasoning here is that it only involved two individuals. Agreed, it involves any two individuals, but it still involves only two individuals. And while a famous physicist joke says that $2+2=5$ for extremely large values of 2, I’d add more rigorously that any integer larger than 2 is larger than 2, even for extremely large values of 2.

I mean that interactions of more than 2 individuals are unimaginably more complex than 2-individual interactions.

Let’s take an extreme case. In quantum mechanics, interactions of any two particles are fundamentally reversible and time has no direction at this level. Meanwhile, in thermodynamics, gases of gazillions of particles are amazingly well described using concepts of irreversibility such as entropy. In other words, as we consider many more particles, emerging phenomena appear which are nowhere to be found in pairwise interactions.

I know! But, with the recent developments of computer science, illustrations of emerging complexities from basic interactions are now uncountable! One of the most famous is Stephen Wolfram’s rule 30. The idea is very simple. You start with a line of white squares, with one black square in the middle. Then, you apply some very simple rule to color your next line: The coloration of a square only depends on the colors of the three squares above (so interactions actually involve 3 components here, not 2). Amazingly, this very basic rule generates overwhelming complexity, which appears random in many (mathematical) senses. But I’ll let Stephen Wolfram explain his discovery, as he does it so much better than I would:

In short, there’s no equivalence between altruism being favor in a population and altruism being favor in pairwise interactions. In other words, Hamilton’s rule doesn’t work in a population of at least three individuals…

The more natural question would be: What would prevent emerging phenomena from appearing? Once again, it’s much more natural for emerging phenomena to appear than to see pairwise interactions dictating all phenomena. However, I’ll still give you 4 reasons which would justify the apparition of emerging phenomena.

Non-Pairwise Interactions

Let’s start with the simplest reason why pairwise interactions don’t dictate group behavior: There may non-pairwise interactions! And I don’t even have to search for complex combinatorial n-individual interactions… Let’s just consider 3 individuals, and apply our rule that 3 is larger than 2, even for extremely large values of 2!

Definitively, yes, as we learn it in game theory! A particularly illustrative example is the 3 miners paradox. In this setting, 2 (and only 2) are needed to bring back gold from the mine. So, any pair of miners benefits by cooperation. However, if all 3 go, then the cooperation of any of the miners is at the disadvantage of the 2 others.

For another illustration of the combinatorial complexity of interactions of 3 individuals, here’s an extract from the awesome TV show Flight of the Conchords, where Dave is strongly affected by the fact that his interaction with a girl was not a 2-individual interaction:

Actually… If you include the fatigue of carrying gold back from the mine, it might be that the cooperation of a miner is at his disadvantage when the two others are already cooperating. Meanwhile, it will always be at the miner’s advantage to cooperate when only one other does. In brief, the combinatorics of the problem suddenly becomes a haunting nightmare! And, crucially, pairwise interactions are completely useless to grasp the dynamics of cooperation.

Yes! At the workshop, van Veelen, in a joint work with Shishi Luo and Burt Simon, presented a model based on a triplet of 3 cooperating individuals being much more capable than a triplet 2 cooperating and 1 defecting ones. Not surprisingly, this model cannot be analyzed with inclusive fitness which cannot describe such phenomena.

Indirect Interactions

Another cause of emerging phenomena is that pairwise interactions have effects on other individuals too (and are thus not really pairwise)! Imagine you saved your cousin from drowning, and that he was in fact your brother’s girlfriend lover. Then, by saving your cousin, you are also weakening your brother’s chances of reproducing. Overall, despite increasing your inclusive fitness in direct pairwise interactions, you are globally weakening the chances of your genes to be passed! More generally, pairwise interactions usually have indirect consequences on third parties.

Granted, indirect interactions are weaker, but, as LinkedIn likes to point it out, there are exponentially many more of them! In fact, an important area of biology and population genetics has involved such indirect interactions to explain the evolution of cooperation. For instance, it has been shown that such interactions can generate positive and negative reputations which would favor altruism.

Yes, indeed. This was beautifully characterized by David Haig as follows:

This might sound restrictive, but Instant Egghead’s vampire bats seem to obey the rules of indirect interactions! Another example appears in mathematician Ernesto Estrada’s recent paper in collaboration with Eusebio Vargas-Estrada, published in Nature, about the influence of such indirect influences on consensus between individuals. Interestingly, it can be applied straightforwardly to gene diversities.

Synergistic Effects

In 1973, John Maynard Smith introduced evolutionary game theory. Since then, ideas of this theory have gained tremendous success, and I invite you to learn more about this topic with this article of mine.

It describes how the dynamics of different populations can evolve, as they interact with one another. Importantly, in this setting, the relative sizes of different populations play a crucial role on their evolution. Typically, imagine two ant colonies fighting for a territory. Then, their genes won’t be nearly as important as the numbers they are. On the opposite, consider an abnormally large population of lions. These will have to compete between one another for food, and their fitness will globally decrease. In both cases, the sizes of populations play a more crucial role, whether it is negatively or positively, than genes. This importance of size is known as the synergistic effect.

Yes! A simple one consists in studying relationship between cooperation and defection. Typically, in a society dominated by cooperation, quite often, cooperation is the best strategy. But if people tend to defect, then it’s usually better not to cooperate. Finally, there may be some equilibrium, where some individuals cooperate while others defect…

A reason for that is if the advantage of being cooperator is smaller than the effects of death and mutation. Indeed, as more people cooperate, it is more likely that the next individual who dies was a cooperator, or that the next individual to mutate is a cooperator who becomes defectors. If these effects surpass the advantages of cooperation around the equilibrium, the equilibrium is even stable! This is known as weak selection. The situation of weak selection is described below:

Yes! And, interestingly, the equilibrium in the middle corresponds to a case of “equal gains from switching” between cooperation and defection. This criterion can be easily translated mathematically, and has been widely used to describe equilibrium states in Nature, including and especially by inclusive fitness theory.

Yes… And if selection isn’t, there may be no equilibrium in the middle! And even if there is, random processes may lead populations to suddenly appear so close either to total cooperation or total defection, that these states will take over the middle equilibrium. In these case, synergistic effects will take over any consideration of inclusive fitness, and concepts like the initial state will be essential. Yet, they are nowhere to be found in inclusive fitness theory.

Social Structures

When we defined relatedness, we had to compare the similarity of an individual with the average of the population. But, which population? If I want to compute the relatedness between two South American people living in the US, do I consider the population they are from, or the population they live in?

I guess so. But still, that’s not an obvious answer, is it? A general approach consists in defining a connectivity of the individuals of the population, and to define relatedness based on this connectivity structure. This structure will then actually be essential to study population dynamics, as explained in this awesome introduction to social networks by Nicholas Christakis on BigThink:

Now, surely enough, when the structure of the population is fixed, it’s possible to define surroundings such that Hamilton’s rule holds (in additive models with weak selection and no indirect influence).

Yes, but there’s worse. What if the structure of the population evolves? Then, relatedness does too, which completely messes up Hamilton’s rule, in a way that it then makes little sense! Yet, arguably, many opportunities of evolution have come from the motions of populations through space, which deeply affects the structure of the populations.

A Bit of Epistemology

I know… But, mathematically, it surely sounds like group selection theory, which consists in studying populations as a whole rather than focusing on pairwise interactions, surely provides something else, which is nowhere to be found in kin selection theory. However, I still applaud and support kin selection.

I’d compare it to Darwin’s tree of life. We now know that (or at least have strong indications of the fact that) life hasn’t really grown like a tree. It’s more like a network of life. Indeed, It seems that life has appeared in multiple places in different ways, and that species have both unmixed and mixed. So, just like kin selection, the idea of a tree of life is inaccurate.

Because, following Hawking’s model-dependent realism, I don’t think science should be about (or, at least, limited to) accurate models of the universe. Newton’s laws of motions and of gravity have been proven wrong, but I’ll still applaud and support them! And that’s because they are useful and insightful.

Yes! Kin selection theory is based on the simple idea of focusing on gene reproductions rather than individuals’. By doing so, it brilliantly explains how altruistic behaviors towards kins can favor the survival of altruism! Obviously, once this is well-known, it’s interesting to go further, but this simple idea is already very powerful to convince people who are not familiar with the details of evolutionary theory of its relevancy and insight! Like in Instant Egghead’s video. Isn’t it what’s most important for a theory?

This is what’s awesomely argued by Sean Carroll as he explains the roles of the fundamental laws of physics on one hand, and of fuzzier but more useful theories of largest structures on the other hand:

One great element of Carroll’s speech is the concept of regime. All theories (even string theory!) are applicable to a certain regime only. An essential responsibility of any theory is to properly define the limits of its regime. Using Sean Carroll’s terminology, the regime of basic inclusive fitness theory requires phenomena like non-pairwise interactions, indirect interactions, synergistic effects and population structure are negligible.

As far as I know, there is no elegant and useful generalization of inclusive fitness in a more general setting. In fact, I’d argue that, just like it’s impossible and irrelevant to derive fluid dynamic equations from quantum mechanics, it’s often much easier and useful to describe population dynamics with group selection rather than deriving it from a generalized version of inclusive fitness theory. This is a general feeling I have, which is largely based on Stephen Wolfram’s examples of cellular automatons and the troubling second law of thermodynamics.

Let’s just say I’m not really fond of an anti-group selection spirit! But, again, I’m not a biologist…

Let’s Conclude

As I’m finishing this article, I can’t help to wonder what Charles Darwin, the father of all these theories, would think about its amazing and controversial new developments. One thing I’m sure of is that he’d be pretty impressed with how much insights genetical theories of population dynamics have yielded. And I kind of think that he’d find our controversies negligible compared to the immensity of what has already been achieved. Recall that, at his time, it wasn’t a mere half of biologists who got things wrong. It was the overwhelming majority.

As I said, they’re both interesting for different reasons, and it’s thus relevant to have both, while understanding the limits of each. But in time, one may well disappear. Now, I doubt any side will ever manage to convince the other to use its approach, but I kind of believe in this quote by German physicist Max Planck.