Take a square sheet of paper. Can you glue opposite sides without ever folding the paper? This is a conundrum that many of the greatest modern mathematicians, like Gauss, Riemann, and Mandelbrot, couldn't figure out. While John Nash did answer yes, he couldn't say how. After 160 years of research, Vincent Borrelli and his collaborators have finally provided a revolutionary and breathtaking example of a bending of a square sheet of paper! And it is spectacularly beautiful!

From the destruction of bridges and buildings to the foundations of electromagnetism and quantum mechanics, through their uses by radios or our ears,resonance is a counter-intuitive underlying phenomenon which shapes our reality. But amazingly, they can be made amazingly visual by playing with head massagers!

In 1988, Euler's identity was elected most beautiful theorem of mathematics. It has been widely taught worldwide. But have you ever stopped to really sense the meaning of this incredible formula? This article does.

In recent years, at the interface of game theory, control theory and statistical mechanics, a new baby of applied mathematics was given birth. Now named mean-field game theory, this new model represents a new active field of research with a huge range of applications! This is mathematics in the making!

In 2006, Pluto was officially demoted from its planetary status. When we dig a little bit, this isn't much of the surprise. What's more interesting is rather why it ever was regarded as a planet, as the History of Pluto highlights a magic enterprise that science is!

We all intuitively think of ourselves as independent creatures with strong free will. However, many disturbing experiments about fashion, conformity, obedience, environment, choice and opinions have been troubling this idea we make of ourselves. These ought to be lessons of humility for all of us.

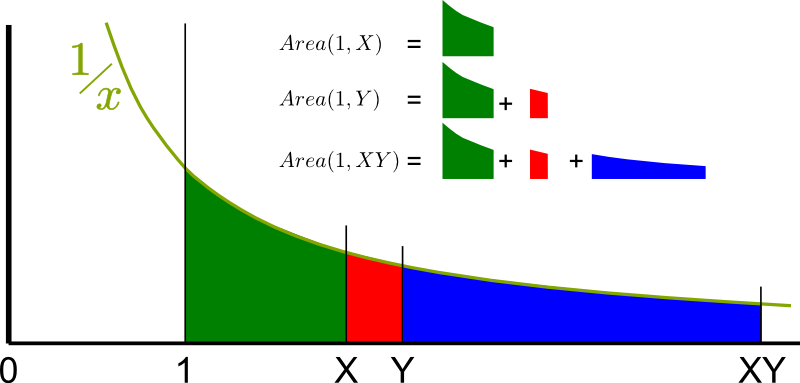
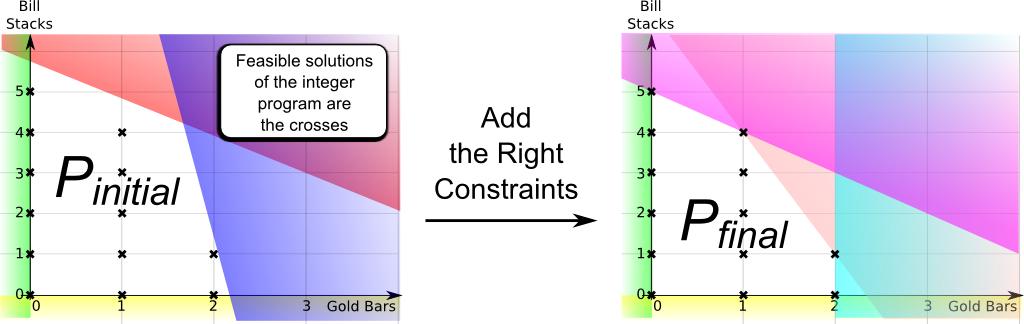
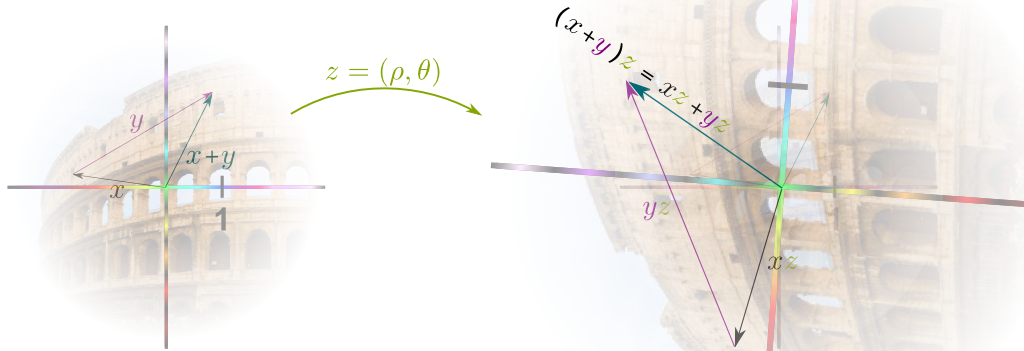
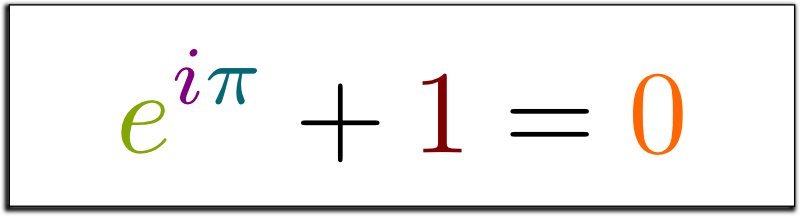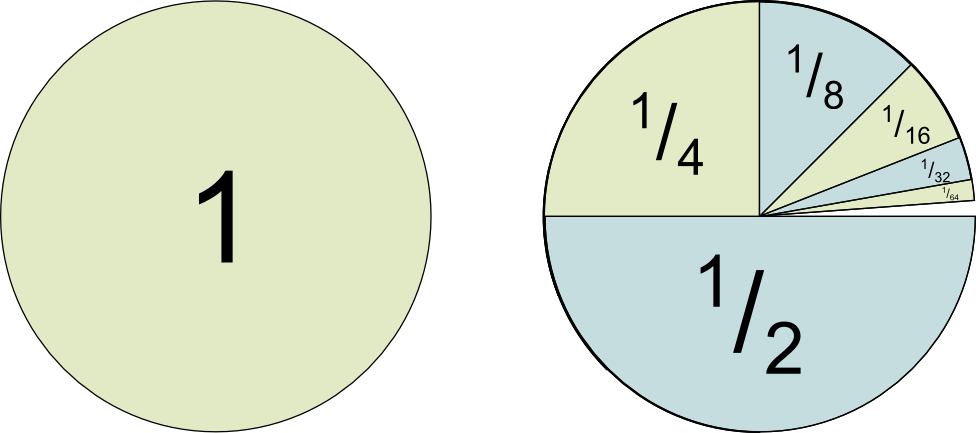In 1832, Évariste Galois died. He was 20. The night before his death, he wrote a legendary letter to his friend, in which he claims to have found a mathematical treasure! Sadly, this treasure had long been buried in total indifference! It took nearly a century to rediscover it! Since then, Galois' legacy has become some of the finest pure mathematics, which represents a hugely active field of research today with crucial applications to cryptography. Galois' work is now known as Galois theory. In essence, it unveils the hidden symmetries of numbers!

Designing routes to visit customers has become one of applied mathematicians' favorite optimization problems, as companies offer millions to solve them! This article discusses the clever technics they have come up with, and use them to help Santa deliver toys to kids all over the world!

In 2010, a controversial article published in Nature violently criticized the last 40 years of developments in evolutionary biology, triggering an ongoing war within the scientific community. This article explains the essence of the controversy!

Linear algebra is a one of the most useful pieces of mathematics and the gateway to higher dimensions. Using Barney Stinson's crazy-hot scale, we introduce its key concepts.

Last summer, I got to discover Morellet's artwork on inclined grids. Amazingly, this artwork is a display of the irrationality of $\sqrt{2}$! It's also a strong argument for the existence of this number. In this article, after discussing that, I take readers further by discussing what numbers can be constructed geometrically, algebraically, analytically or set theoretically using the power of mathematics!

The second law of thermodynamics is my favorite law in physics, mainly because of the troubling puzzles it raises! Indeed, what your professors may have forgotten to tell you is that this law connects today's world to its first instant, the Big Bang! Find out why!

Amusingly, the age difference between a 45-year-old man and a 25-year-old woman doesn't seem as big as the age difference between them 20 years earlier, when the woman was a little 5-year-old girl. This remark was the insight the late science popularizer Albert Jacquart liked to give to his readers to explain logarithms. This article pays tribute to the great scientist by introducing age difference as he liked to tell it.

Integer programming is arguably the greatest achievement of applied mathematics. Half of the time, it's what's used to solve real-world problems!

My first reaction to imaginary numbers was... What the hell is that? Even now, I have trouble getting my head around these mathematical objects. Fortunately, I have a secret weapon: Geometry! This article proposes constructing complex numbers with a very geometrical and intuitive approach, which is probably very different from what you've learned (or will learn).

According to Matthew Colless, the most important aspect of science is beauty. Not only is it what inspires scientists and their quests, I'd even claim that it's also the compass that guide them in their quests, in a deeper and more surprising way that one can imagine!

Our eyes are amazing! Even today's cameras are nowhere near competing with them. However, the recent development of high dynamic range (HDR) and tone mapping technologies creates new possibilities to get images nearly as awesome as what our eyes really see!

The conic sections, that is, ellipses, parabolas and hyperbolas, are too often presented analytically. Yet, their amazing beauty is actually their spectacular geometry, as well as their omnipresence! This article presents plenty of illustrative descriptions of their uncountable applications!

1+2+4+8+16+...=-1, as proven by Henry Reich on Minute Physics! Now, as a mathematician, I must say that his proof is far from being rigorous. In fact, anyone familiar with the surprising flavor of infinite series should not find it convincing. Surprisingly though, his proof can be rigorously and naturally justified! Find out how!

I was a kid when I was first introduced to the deceptively simple utilities problem. It's only lately that I've discovered its solution! And it's an amazing one! Indeed, it provides a wonderful insight into some fundamental mathematics, including Euler's formula! This is nothing less than the gateway to the wonderful world of algebraic topology!